Уведомления
Авторизуйтесь или зарегистрируйтесь, чтобы оценивать материалы, создавать записи и писать комментарии.
Авторизуясь, вы соглашаетесь с правилами пользования сайтом и даете согласие на обработку персональных данных.
ИИ научился легко решать сложнейшие уравнения, которые описывают устройство Вселенной
Дифференциальные уравнения в частных производных встречаются в самых разных аспектах физико-математического моделирования. Они позволяют рассчитывать состояния весьма сложных систем, но их решение всегда было ресурсоемкой задачей. Благодаря специально созданной нейросети этот процесс значительно ускорился и мощности суперкомпьютеров можно будет перенаправить на другие важные задачи.
Большинство студентов технических специальностей встречают уравнения математической физики (УМФ), или дифференциальные уравнения в частных производных, лишь однажды. Пройдя их во время обучения, об этом сложном, но мощном инструменте почти всегда забывают. И лишь некоторые инженеры используют их регулярно. Речь идет, например, о моделировании воздушных потоков в аэродинамике, описании движения тектонических плит, расчете положения планет или метеорологии.
Как правило, для решения подобных уравнений применяют мощные вычислительные комплексы — суперкомпьютеры или сети распределенных вычислений. Для многих ученых, работающих в не самых богатых на финансирование отраслях, такие расчеты всегда были головной болью. Понимая важность появления нового инструмента для выполнения подобных задач, американские математики и программисты обратились к технологиям искусственного интеллекта.
Коллектив ученых из Калифорнийского технологического института (Caltech) и Университета Пердью разработал высокоэффективный нейросетевой алгоритм для работы с УМФ. При его использовании удалось достичь огромного прироста скорости решения уравнений — в некоторых случаях на несколько порядков. Например, на матрице 256х256 их Нейронный оператор Фурье (Fourier neural operator, FNO) выдал результат за 0,005 секунды при решении уравнений Навье — Стокса. Наиболее распространенный алгоритм, используемый ранее, рассчитывал те же условия за 2,2 секунды.
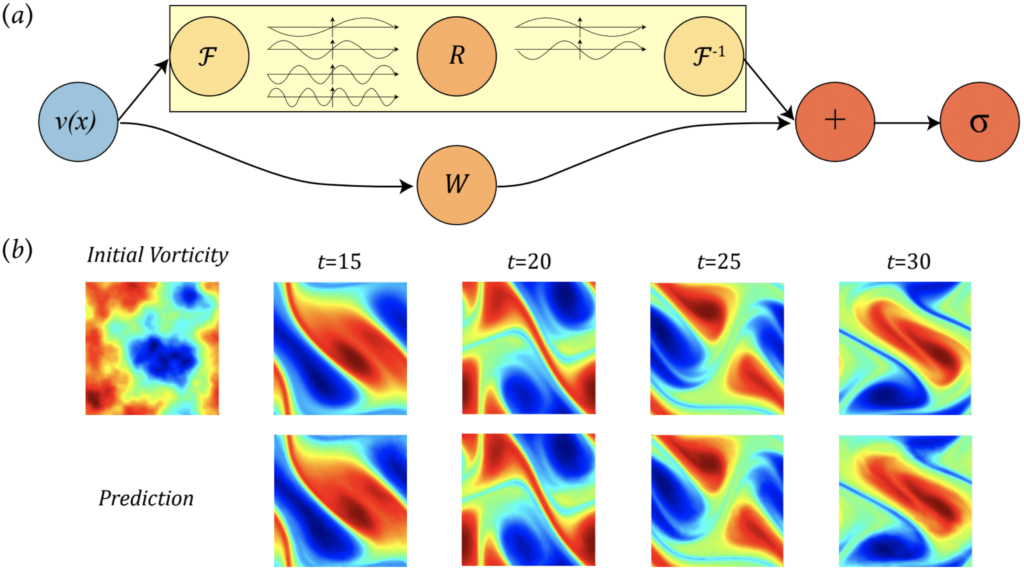
Эти дифференциальные уравнения встречаются повсеместно — точнее, с их помощью можно описать практически любую динамическую систему. Появление доступного и эффективного метода их решения может существенно продвинуть вперед самые разные области науки. А уж применимость такого «искусственного интеллекта» в инженерных разработках точно не заставит себя ждать. Полное описание своей работы американские ученые опубликовали на портале arXiv.
Нельзя сказать, что создатели FNO первыми догадались решать дифференциальные уравнения в частных производных с помощью нейросетей и машинного обучения. Нет, так делали и раньше. Однако существующие алгоритмы приходилось обучать заново на каждый новый набор вычислений — даже при изменении свойств похожих жидкостей. Разработка ученых из Калтеха и Пердью позволяет выполнить «тренировку» лишь однажды и обсчитывать самые разные модели. Секрет эффективности FNO гениален и одновременно прост.
Основа работы любой нейросети — аппроксимация функции, ее приближение. Искусственный интеллект оперирует в своих вычислениях не точными значениями, а диапазоном величин, который позволяет принять решение или выдать результат, не прибегая к ресурсоемким и сложным уточнениям. Иными словами, нейросети во время обучения вырабатывают упрощенные формулы, результаты которых достаточно точны, чтобы применяться на практике.
Обычно работающие с графиками функций нейросети оперируют значениями в евклидовом пространстве. Для того чтобы упростить задачу, авторы FNO решили не переводить волновые функции в привычные графики, а «научить» алгоритм работать напрямую с преобразованиями Фурье. Это позволило не только прибавить скорость вычислений, но и снизить количество ошибок: их теперь на 30% меньше, чем в прежних алгоритмах.
Telegram 
Дзен 
VK Согласно гипотезе о так называемой Еврогондване, в эпоху динозавров Европа, как часть северного суперконтинента Лавразия, еще не полностью отделилась от южного суперконтинента Гондвана и животные могли свободно мигрировать между Европой и Африкой. Однако новый анализ найденных в Венгрии костей первобытного крокодила показал, что его сходство с гондванскими видами обусловлено не близким родством, а схожим образом жизни.
Треть века назад Штаты и Мексика подписали Североамериканское соглашение о свободной торговле. Авторы новой научной работы показали, что это спровоцировало рост войн между бандами и подъем смертности среди молодых мужчин на десятки процентов — но только в тех зонах, которые были интересны картелям. Всего после подписания соглашения в Мексике было убито (оценка с учетом исчезнувших трупов) более 0,85 миллиона человек.
Новые данные показали, что удар зонда DART не только изменил орбитальный период небольшого спутника Диморфа вокруг его «родителя» Дидима, но и вызвал небольшое изменение движения всей бинарной системы вокруг Солнца. Эти результаты укрепляют уверенность ученых в том, что технология кинетического удара, при заблаговременном обнаружении опасного объекта, может помочь отклонить потенциально опасный астероид от столкновения с Землей.
Одна сторона сыплет более дорогими и сложными баллистическими ракетами, другая — относительно дешевыми крылатыми. Но при этом первая на порядок беднее второй. А что у них с технологическим уровнем для наземной войны, и почему, кстати, глава второй избегает даже самого этого слова? Попробуем разобраться в реальных возможностях военных машин сторон потенциально самого опасного конфликта 2026 года.
Запасы лития в России требуют переоценки и могут оказаться в разы выше, чем считалось до 2025 года. Об этом говорится в исследовании «Состояние ресурсной базы критически важных металлов и элементов для развития современных технологий», подготовленном учеными РГУ нефти и газа (НИУ) имени И.М. Губкина.
Российские ученые из МФТИ с коллегами из Института прикладной математики им. М. В. Келдыша РАН и Института физики Земли им. О.Ю. Шмидта РАН разработали инновационный метод для расчета равновесного распределения несмешивающихся жидкостей в пористой среде. Результаты применения этого метода можно использовать в разработках по повышению нефтеотдачи и гидрологии, а также геологического СО2-хранения.
Астрономы недавно проанализировали базу данных о падающих на Землю объектах и пришли к выводу, что два из них прибыли из межзвездного пространства. Известна не только дата, но и место падения каждого из них.
В ноябре 2025 года при взлете российской ракеты с Байконура к МКС с существенной высоты упала кабина обслуживания 8У216. Поскольку в 2010-х годах из экономии средств у нас отказались от дублирования стартовых площадок, это создало ситуацию временной невозможности пилотируемых полетов. Теперь, всего через три месяца после происшествия, «Роскосмос» смог решить проблему, поставив запасную кабину обслуживания, найденную на складах Минобороны. Весенние пуски к МКС, запланированные ранее, теперь имеют шансы пройти в срок.
«Любить лишь можно только раз», — писал поэт Сергей Есенин, а герои культовых сериалов приходили к выводу, что «настоящая» влюбленность случается в жизни максимум дважды. Однако ни один из этих тезисов не подкреплен научными данными. Американские исследователи подошли к вопросу иначе: опросили более 10 тысяч человек и вывели среднее число сильных влюбленностей, возможных в течение жизни.
Вы попытались написать запрещенную фразу или вас забанили за частые нарушения.
Понятно
Из-за нарушений правил сайта на ваш аккаунт были наложены ограничения. Если это ошибка, напишите нам.
Понятно
Наши фильтры обнаружили в ваших действиях признаки накрутки. Отдохните немного и вернитесь к нам позже.
Понятно
Мы скоро изучим заявку и свяжемся с Вами по указанной почте в случае положительного исхода. Спасибо за интерес к проекту.
Понятно
Последние комментарии