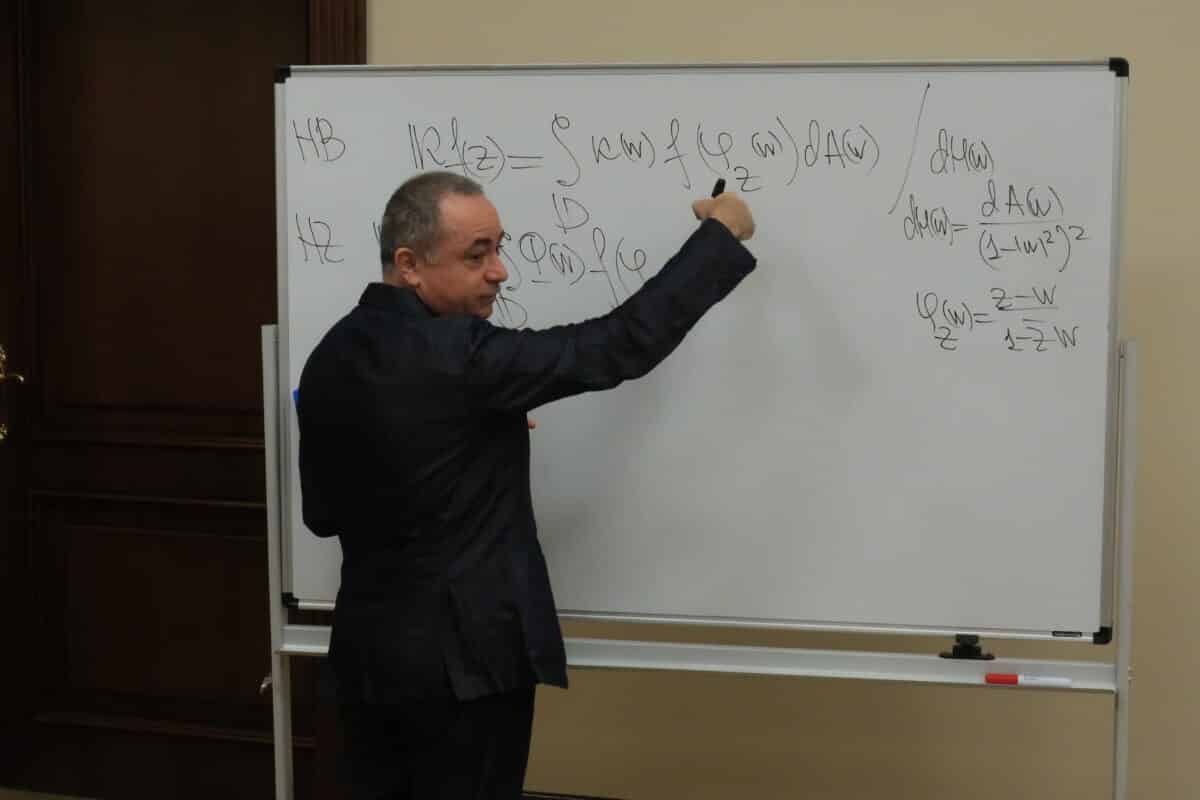Уведомления
Авторизуйтесь или зарегистрируйтесь, чтобы оценивать материалы, создавать записи и писать комментарии.
Авторизуясь, вы соглашаетесь с правилами пользования сайтом и даете согласие на обработку персональных данных.
В ЮФУ нашли новый подход к определению больших и малых пространств Лебега
Применение теории экстраполяции в определении больших и малых пространств Лебега открывает перспективы для новых направлений в математике. Ученые ЮФУ ожидают, что их исследование станет отправной точкой для развития новых теорий и методов в этой области, что поможет решать сложные проблемы с высокой точностью и эффективностью.
В математике, при решении реальных задач и построении математических моделей, функции играют ключевую роль. Известные нам со времен школы, они представляют собой не только абстрактные концепции, но и основу для описания физических процессов и явлений. Так, сегодня ученые используют в своих исследованиях совокупность таких функций, объединенных по некоторому признаку, которые в математике называют классами или пространствами функций. Для чего же это нужно? Функции могут описывать как начальные (исходные) условия, например температуру, скорость или положение объекта в начальный момент, так и само решение задачи, характеризующее конкретный физический процесс в зависимости от времени или от других параметров.
В обычной жизни мы привыкли работать с обычными числами, например, средней температурой или максимальной. Однако, иногда нам нужно уметь измерять глобальные характеристики объектов (функций), которые могут варьироваться по разным параметрам, например, по времени или по местоположению. Пространства Лебега как раз предоставляют инструменты для работы с такими сложными функциями: вместо того, чтобы просто смотреть на значения функции в конкретных точках, мы можем анализировать их в целом, учитывая их распределение, вариации и другие характеристики. Это особенно важно, например, при анализе физических процессов, которые описываются не в каждый момент времени, а некоторыми глобальными данными.
Интересно, что все функции, которые мы строили на графиках в школе, существуют в так называемом банаховом пространстве – нормированном векторном пространстве, полностью определенном нормой. В зависимости от области применения существуют разные подходы к тому, какие законы геометрии работают в этом пространстве: эвклидова геометрия, геометрия Лобачевского и так далее. При этом все функции, у которых интегрируется степень, существуют в Лебеговом пространстве. Однако работа с функциями в этом пространстве может быть сложной из-за его особых математических законов, поэтому математики давно пытаются упростить расчеты в нем.
В Южном федеральном университете над этой проблемой работает директор Регионального научно-образовательного центра ЮФУ Алексей Карапетянц. «В процессе построения математической модели зачастую приходят к интегральным уравнениям, в которых фигурируют эти самые функции. Но также часто оказывается, что геометрия исходного объекта не очень хороша для последующих приближенных вычислений, ввиду чего прибегают к искажению исходного пространства — замене координат.
При этом изучаемые объекты (области интегрирования) преобразуют в более подходящие для применения численных методов. Но это искажение пространства влечет за собой появление некоторого множителя в интеграле, отвечающего за это искажение, после чего вся подынтегральная конструкция может перестать быть интегрируемой из-за появления дополнительной особенности», – рассказал Алексей Карапетянц.
Ученый также отметил, что выходом было бы расширить исходное пространство функций так, чтобы после добавления этой особенности полученный объект продолжал бы оставаться в исходном классе функций, то есть быть интегрируемым. С другой стороны, расширение означает загрубление последующего результата, поэтому нужно обеспечить такое расширение, которое бы было больше исходного, но одновременно это расширение было бы практически «неуловимым».
Здесь в работу вступает так называемый «инфинитезимальный анализ», или анализ «бесконечно малых», некоторая философия математики, которая привычна для математиков уже много столетий, но в современном мире трактуется как что-то новое в приложениях и смежных областях наук.
Собственно, таким образом и появилось понятие «больших» пространств Лебега, которые больше самих классических пространств Лебега, но эта разница неуловима, если пытаться ее «измерить». Эти пространства функций возникли в работах Карло Сбордоне (Италия) и Тадеуша Иванеца (США/Польша) в начале 1990 годов. Однако предпосылки были получены в более ранних работах Николая Карапетянца и Бориса Рубина (РГУ, ныне-ЮФУ).
В новой работе, результаты которой опубликованы в журнале Mathematical Methods in the Applied Sciences, Алексей Карапетянц в соавторстве с математиком из Ярославля, партнером Математического Центра ЮФУ- Евгением Бережным, предлагает новую модель построения Больших пространств Лебега путем экстраполяции – хорошо знакомой математической операции.
«Наша работа является расширением уже классической теории на некоторые предельные показатели. Мы использовали новый в данном контексте метод, основанный на теории экстраполяции, то есть, когда математически «прогнозируются» свойства нового объекта на основе некоторого предельного перехода (экстраполирования). Данный подход позволяет проводить исследование в существенно более общей постановке, то есть обеспечивает унифицированную модель для широкого класс объектов», – объяснил ученый.
Ожидается, что это исследование откроет новые горизонты в теории больших и малых пространств Лебега, предоставляя математикам новые инструменты для анализа и решения сложных задач в различных областях науки и техники.
Telegram 
Дзен 
VK Международная команда исследователей с участием ученых из НИУ ВШЭ экспериментально показала, что люди, страдающие биполярным расстройством, считают мир более нестабильным, чем он есть на самом деле, и из-за этого чаще принимают нерациональные решения. Ученые предполагают, что полученные результаты позволят в будущем разработать более точные методы диагностики и терапии биполярного аффективного расстройства.
Просмотры вакансий и подача заявлений о поиске нового места работы резко активизировались в среде американских ученых, причем они ищут места вне Штатов. Происходящее связано даже не столько с сокращением финансирования науки новой администрацией, сколько с неуверенностью в том, что того или иного исследователя сокращения не коснутся в будущем.
Расчеты показывают, что значительная часть обычной материи содержится не в звездах и планетах, а в межгалактическом пространстве. Это крайне разреженное вещество невозможно наблюдать напрямую, но ученые нашли подходящий «инструмент» — быстрые радиовсплески. В новом масштабном исследовании астрономы изучили более полусотни таких событий и выявили «потерянную» материю Вселенной.
Изучив поведение 69 видов птиц в разных областях Западных Гат (Индия), международная исследовательская группа наконец объяснила, почему территориальные и всеядные птицы чаще других поют по утрам.
Наблюдая ранние этапы рождения землеподобных миров, астрономы приблизились к решению «метрового барьера» — проблемы роста пылевых зерен до размеров, необходимых для формирования планет.
Среди ныне живущих морских обитателей осталось всего несколько так называемых «живых» ископаемых вроде латимерии или мечехвоста. Остальных мы знаем по уцелевшим остаткам. Новый вид древней рыбы обнаружили палеонтологи в девонском песчанике Канадской Арктики. Судя по найденным зубам и челюстям, рыба была в разы меньше своих родственников, а значит, могла жить в реках, что необычно для этих существ.
Вид антилоп, с ледникового периода привыкший к массовым миграциям, пытается вернуться в свой исторический ареал, когда-то достигавший Днепра. Однако их нетипичные для травоядных привычки вызывают сильнейшее отторжение у сельских жителей, предлагающих массово уничтожать их с воздуха. С экологической точки зрения возвращение этих животных весьма желательно, но как примирить их с фермерами — неясно.
Недавно вышел второй сезон сериала «Одни из нас» (TheLastofUs), созданного по сюжету популярнейшей видеоигры. Ученые Пермского Политеха решили разобраться, насколько реален сценарий грибной пандемии, превращающей людей зомби? Чем живет кордицепс и как он «ищет» своих жертв, действительно ли паразит способен эволюционировать настолько, чтобы поражать человеческий организм и подчинять себе его волю, был бы у людей шанс выжить, какие грибы уже поселились в наших телах и выручит ли нас иммунитет, сформированный тысячелетиями.
Казахстанский Алматы — город контрастов, где горы соседствуют с урбанистическими пейзажами, а бизнес-центры — с историческими кварталами. Неизменным остается одно — пробки. Ежедневно сюда приезжает более 700 тысяч автомобилей из пригородов, при этом в самом мегаполисе зарегистрировано порядка 600 тысяч транспортных средств. В результате по улицам ежедневно движется более миллиона транспортных средств.
Вы попытались написать запрещенную фразу или вас забанили за частые нарушения.
Понятно
Из-за нарушений правил сайта на ваш аккаунт были наложены ограничения. Если это ошибка, напишите нам.
Понятно
Наши фильтры обнаружили в ваших действиях признаки накрутки. Отдохните немного и вернитесь к нам позже.
Понятно
Мы скоро изучим заявку и свяжемся с Вами по указанной почте в случае положительного исхода. Спасибо за интерес к проекту.
Понятно