Математик нашел способ решить дифференциальное уравнение, считавшееся нерешаемым с XIX века

В средней школе на уроках математики учат, что для нахождения x в уравнении ax2+bx+c=0 нужно просто подставить коэффициенты a, b и c в готовую формулу вычисления корня уравнения через дискриминант. Это удобно, быстро и понятно. Однако в высшей математике, в которой описываются сложные процессы, используются уравнения вида ay»+ by’+cy=g.  Это тоже уравнение второго порядка, но не алгебраическое, а дифференциальное.

Представьте, что вы едете на машине. Если дорога идеально ровная, а скорость постоянная, рассчитать время в пути легко. Это задача с постоянными коэффициентами. А теперь представьте, что покрытие дороги постоянно меняется, ветер дует с разной силой, угол наклона горы под колесами все время разный. В таких условиях ваша скорость и время зависят от множества меняющихся факторов.

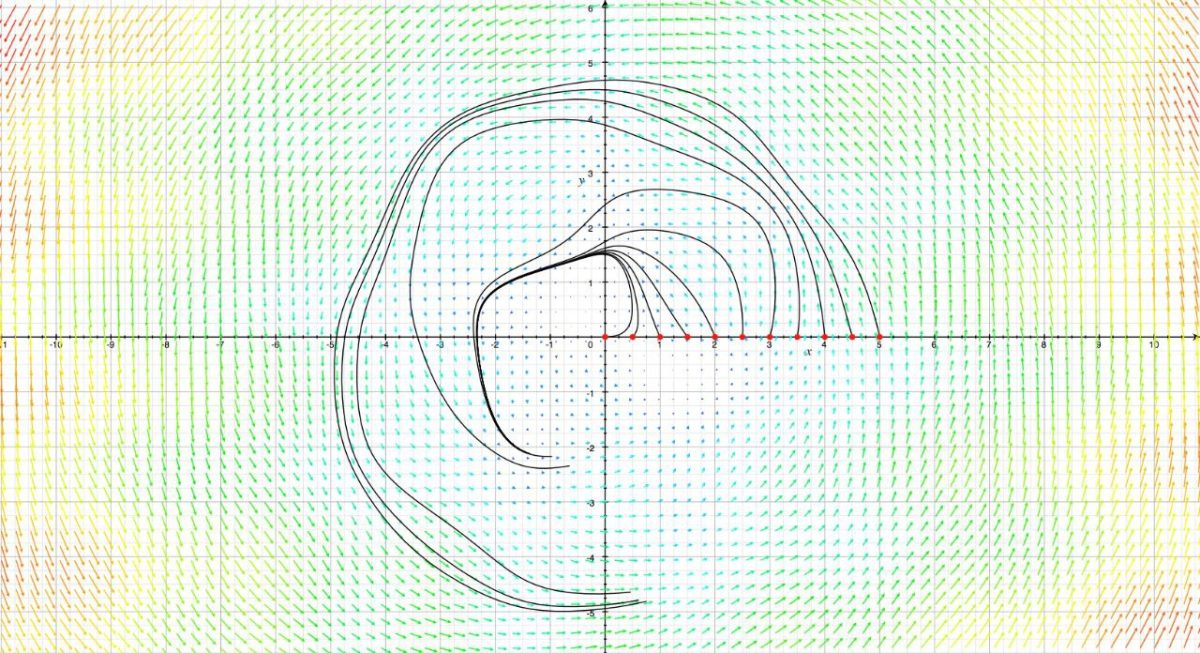
Математически это описывается дифференциальными уравнениями второго порядка. В них на месте обычных чисел в качестве коэффициентов стоят функции — величины, которые сами постоянно меняются. А вместо простого возведения в квадрат стоит операция вычисления второй производной — математический аналог того, как резко машина разгоняется или тормозит.

Такие уравнения — это фундаментальный инструмент науки: они описывают все — от колебаний маятника и сигналов в электросетях до движения планет. И именно здесь исследователи зашли в тупик. Еще в 1834 году французский математик Жозеф Лиувилль показал, что невозможно выразить решение такого уравнения через его коэффициенты, используя стандартный набор действий: сложение и вычитание, умножение и деление, а также элементарные функции, такие как корни, логарифмы, синус, косинус, и интегралы. С тех пор в математическом сообществе укоренилось мнение, что общей формулы для их решения нет и быть не может. Задача считалась закрытой и безнадежно неразрешимой более 190 лет. Простую формулу, похожую на формулу решения квадратного уравнения через дискриминант, давно перестали искать для дифференциальных уравнений.

Старший научный сотрудник НИУ ВШЭ и ИППИ РАН Иван Ремизов предложил изящный выход. Он не стал спорить с Лиувиллем, а просто расширил набор инструментов. К стандартным математическим действиям ученый добавил еще одно — нахождение предела последовательности. Это позволило записать формулу, в которую можно подставить коэффициенты a, b, c и g уравнения ay»+ by’+cy=g, и найти его решение — функцию y. Результаты работы опубликованы во Владикавказском математическом журнале.

Метод основан на теории аппроксимаций Чернова. Суть идеи в том, что сложный, постоянно меняющийся процесс разбивается на бесконечное множество простых шагов. Для каждого такого участка строится свое приближение — элементарный фрагмент, который описывает поведение системы в конкретной точке. По отдельности эти кусочки дают лишь упрощенную картину, но, когда их число устремляется к бесконечности, они бесшовно соединяются в идеально точный график решения. Скорость сходимости приближений к точному решению можно найти с помощью оценок, которые Иван Ремизов получил вместе с коллегой Олегом Галкиным в прошлом году.

В новой статье Ремизова доказано: если применить к этим шагам преобразование Лапласа — метод, который переводит задачу с языка сложных изменений на язык обычных алгебраических вычислений, — они безошибочно фокусируются в итоговый результат. Ученые называют его резольвентой. 

«Представьте, что искомое решение уравнения — это большая картина. Рассмотреть ее сразу целиком очень трудно. Но математика умеет отлично описывать процессы, развивающиеся во времени. Результатом работы стала теорема, которая позволяет “нарезать” этот процесс на множество маленьких простых кадров, а затем с помощью преобразования Лапласа собрать из этих кадров единую статичную картину — решение сложного уравнения, то есть резольвенту. Проще говоря, вместо того, чтобы гадать, как выглядит картина, теорема позволяет восстановить облик, быстро прокручивая “киноленту” ее создания», — объясняет автор работы, старший научный сотрудник Международной лаборатории динамических систем и приложений НИУ ВШЭ в Нижнем Новгороде Иван Ремизов. 

Дифференциальные уравнения второго порядка используются не только для моделирования событий реального мира, но и для определения новых функций, которые нельзя задать иным образом. К ним относятся, например, так называемые специальные функции Матье и Хилла, они критически важны для понимания того, как движутся спутники на орбите или протоны в Большом адронном коллайдере.

«Единственное рабочее определение таких функций заключается в том, что они являются решениями конкретных сложных уравнений. Это как если бы вы не знали имени человека и могли описать его только через работу. Например: тот человек, который водит красный автобус по пятому маршруту. Понятно, о ком идет речь, но на практике не помогает обратиться к нему по имени», — поясняет Иван Ремизов.

Предложенный автором подход позволяет выражать решения уравнений через их коэффициенты напрямую. Благодаря этому специальные функции теперь можно задавать явными формулами подобно тому, как формула y(x)=x2 задает функцию y. Чтобы найти y(x) из этого примера, нужно число х умножить само на себя. Разумеется, для функций Матье и Хилла формулы имеют более сложную структуру, но принцип тот же: слева от знака равенства стоит величина, которую нужно найти, а справа указаны явные действия, выполнение которых приведет к ее нахождению.

При этом работа Ивана Ремизова перекидывает мостик от математики к современной физике. Ученый впервые представил решение обыкновенного дифференциального уравнения в виде формулы, аналогичной знаменитым интегралам нобелевского лауреата Ричарда Фейнмана, с помощью которых описывают движение квантовых частиц. То, что раньше работало для квантовой механики, теперь применимо к классическим задачам.

НИУ ВШЭ

535 статей

Национальный исследовательский университет «Высшая школа экономики» — один из крупнейших и самых востребованных вузов России. В университете учится 54 тысячи студентов и работает почти 4,5 тысячи учёных и преподавателей. НИУ ВШЭ ведёт фундаментальные и прикладные исследования в области социально-экономических, гуманитарных, юридических, инженерных, компьютерных, физико-математических наук, а также креативных индустрий. В университете действуют 47 центров превосходства, или международных лабораторий. Вышка объединяет ведущих мировых исследователей в области изучения мозга, нейротехнологий, биоинформатики и искусственного интеллекта. Университет входит в первую группу программы «Приоритет-2030» в направлении «Исследовательское лидерство». Кампусы НИУ ВШЭ расположены в четырех городах — Москве, Санкт-Петербурге, Нижнем Новгороде и Перми, а также в цифровом пространстве — «Вышка Онлайн».

Показать больше

Закладка

Скопировать ссылку

Email

Печать

Twitter

VK

Telegram