Уведомления
Авторизуйтесь или зарегистрируйтесь, чтобы оценивать материалы, создавать записи и писать комментарии.
Авторизуясь, вы соглашаетесь с правилами пользования сайтом и даете согласие на обработку персональных данных.
Дела на миллион: математические «Задачи тысячелетия» доступным языком
Август 1900 года ознаменовался проведением в Париже II Международного конгресса математиков, на котором один из корифеев науки Давид Гильберт сформулировал наиболее кардинальные проблемы, требующие разрешения. 23 проблемы Гильберта определили многие ключевые направления развития математики в прошлом столетии.
К началу XXI века почти все они были решены, либо покинули список по другим причинам – например, как нечетко сформулированные, – и сто лет спустя после Гильберта математик Стивен Смейл выдвинул новый список 18 проблем, стоящих перед математиками и физиками нашего времени. Попытку Смейла можно засчитать, однако куда большую известность получил альтернативный вариант, предложенный авторитетным американским институтом Клэя. Семь проблем были названы на громком мероприятии, специально организованном в Париже. Одна из них, гипотеза Римана, перекочевала еще из списка 1900 года, а еще одна – гипотеза Пуанкаре – оказалась доказанной уже два года спустя.
Naked Science представляет краткий обзор «Задач тысячелетия», за решение каждой из которых институт Клэя готов выплатить миллион долларов. Кстати, это касается и гипотезы Пуанкаре: заслуженный миллион по-прежнему ожидает выплаты, и пока что Григорий Перельман отказывается принять награду. Разумеется, мы упростили многие моменты, постаравшись объяснить задачи так, чтобы суть была понятной даже человеку, совсем далекому и от высшей, и какой-либо другой математики.
1. Равенство классов P и NP
Область: теория алгоритмов
Предположено в начале 1970‑х, остается нерешенным
Представьте, что вам надо закупить офисной техники, мебели и канцтоваров на 500 тыс. рублей – и вы просматриваете прайс-лист поставщика. Вы можете выбрать, что хотите, но в списке обязательно должны быть два принтера, одно кресло руководителя, 50 шариковых ручек, остальное по желанию. Сколько комбинаций возможно? Это вариант «задачи о ранце», которая в классическом виде состоит в том, чтобы уложить в объем рюкзака как можно больше вещей определенного объема и стоимости. Проверить конечный вариант легко, но найти его сложно. К этим задачам, кстати, относится и «вскрытие» чужого пароля, который шифруется таким образом, что система может легко проверить его корректность, но взломщику практически невозможно вычислить правильный вариант в море альтернативных решений зашифрованной строки.

Такие проблемы в теории алгоритмов относятся классу сложности NP: их решение можно быстро проверить. Часть из них входят в класс P – те, решение которых еще и легко находится (за «обозримое», или, строже говоря, полиномиальное время). Вопрос состоит в том, всегда ли существуют простые алгоритмы решения NP-задач – то есть, равны ли классы NP и Р. Сегодня предполагается, что ответ на него будет отрицательным: далеко не все задачи, решения которых легко проверяемы, могут быть легко решаемы. Математик из NASA Субит Чакрабарти прогнозирует, что окончательный ответ может быть получен в течение ближайших 50 лет.
2. Существование и гладкость решений уравнений Навье — Стокса
Область: математическая физика (гидродинамика)
Задача известна более ста лет, остается нерешенной
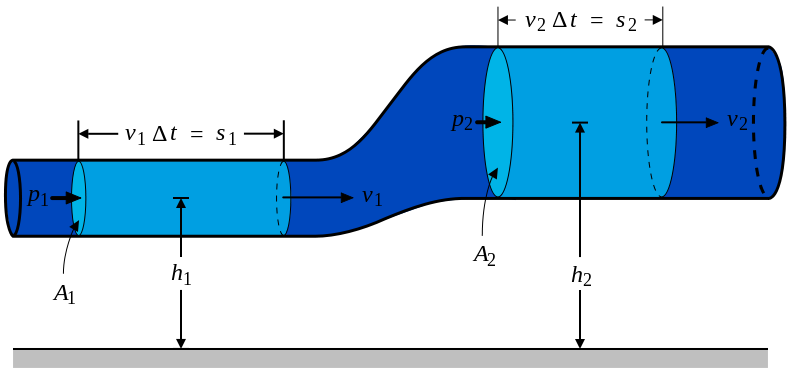
Задача на стыке математики и классической физики вырастает из работ, проделанных еще в XIX в., когда ученые стали формулировать строгие законы, которые описывают движение жидкостей. Полученные тогда уравнения Навье – Стокса остаются одними из важнейших в гидродинамике и аэродинамике. Они позволяют вычислять скорость потока с учетом вязкости, сжимаемости, плотности, давления и т. п., и используются повсеместно. Однако решить их в общем виде до сих пор не удается, и расчеты ведутся лишь для отдельных, частных случаев.
В решении уравнений Навье – Стокса скрываются многие тайны одного из самых «твердых орешков» современной физики – проблемы турбулентности. С ней современные технологии встречаются повсеместно, от самолетов и подлодок до ветряных электростанций и автомобилей, – но во многом турбулентность остается плохо понятной, плохо просчитываемой и почти непредсказуемой. Поэтому ученые штурмуют эту «Задачу тысячелетия» с особенным упорством. Математик Субит Чакрабарти предполагает, что в течение полувека решение сложных уравнений турбулентности может быть найдено.
Пока же заявку на победу подал казахстанский математик Мухтарбай Отелбаев, в расчетах которого впоследствии была найдена ошибка, а также узбекский ученый Шокир Довлатов, решение которого еще проверяется. Американский математик Стивен Смейл – лауреат премии Филдса за работы в области топологии. В 2000 г. он возглавлял факультет математики в Калифорнийском университете в Беркли, когда академик Владимир Арнольд – тогда еще президент Международного математического союза (IMU) – предложил ему подобрать список новых проблем на смену уже выполнившему свои задачи списку Гильберта. Смейл подобрал 18 таких задач, из которых некоторые, включая равенство Р и NP, гипотезы Пуанкаре и Римана, решения уравнений Навье – Стокса и т. д., вошли и в список «Задач тысячелетия», подготовленный институтом Клэя.
3. Гипотеза Римана
Область: теория чисел
Сформулирована в 1859 г., остается нерешенной
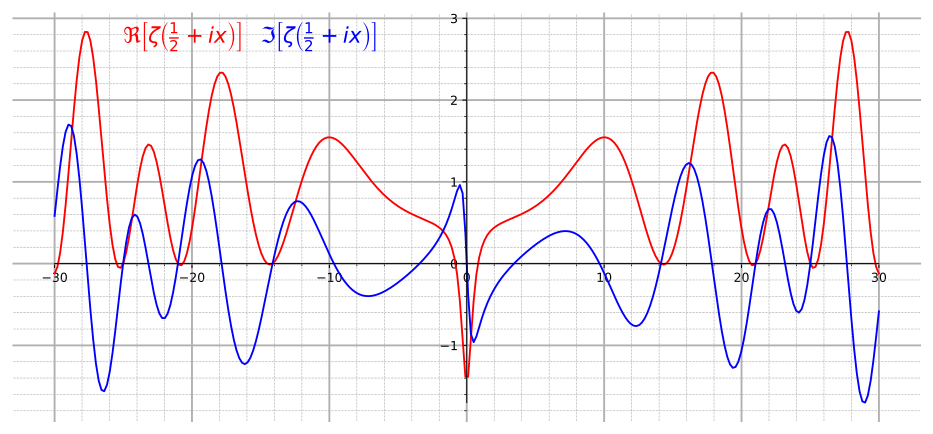
Многие из нас еще со школы помнят о существовании простых чисел – тех, которые делятся только на 1 и на самих себя, как 2, 3, 5, 7, 11 и т. д. Простые числа играют важную роль и в «абстрактной» теории чисел, и в практике – например, в работе криптографических алгоритмов. Если отметить положение всех простых чисел на числовой оси, то мы увидим, что их распределение неравномерно и, кажется, не подчиняется какой-то закономерности, поэтому заранее предсказать, где именно появится следующее простое число, не получается. Однако Бернард Риман показал, что это распределение похоже на точки, в которых дзета-функция – ς(s) = 1/1s + 1/2s + 1/3s + 1/4s + … – обращается в ноль.
Известно, что нулевое значение она имеет, когда s – отрицательное четное число. Но где еще? Согласно выкладкам Римана, другие нули появляются, если s – комплексное число, содержащее действительную часть 1/2. Задача была названа в числе актуальных еще Давидом Гильбертом в 1900 г. и не решена до сих пор, хотя практически все математики готовы согласиться: расчеты, проведенные даже с использованием суперкомпьютеров и для невероятно громадных простых чисел, подтверждают справедливость гипотезы Римана. Она доказана для примерно 10 трлн первых решений, но в общем виде пока – нет. По словам Субита Чакрабарти, за годы работы над этой проблемой математики продвинулись достаточно далеко, и ответ может быть найден в ближайшие десятилетия.
4. Гипотеза Пуанкаре
Область: топология
Появилась в 1900–1904 гг., решена в 2002 г.
Гипотеза Пуанкаре относится к топологии – одной из самых сложных и молодых областей математики, которая исследует свойства геометрических фигур и их деформаций, происходящих без разрыва. Слепите из пластилина пирамиду – вы легко превратите ее в конус, цилиндр или даже сферу, нигде ничего не склеивая и не разрывая. Слепите бублик – и такой трюк вам уже не удастся, хотя бублик легко деформируется, например в чашку с ручкой. Говоря строже, поверхности сферы и цилиндра гомеоморфны, а сферы и тора – негомеоморфны. Но это для простейшего случая: то, что любая замкнутая (без дырок) двухмерная поверхность гомеоморфна двухмерной сфере, показал еще Пуанкаре. Решение для поверхностей более высоких размерностей потребовало около века.
Интересно, что для размерностей 5 и выше гипотеза Пуанкаре была доказана еще в 1960-х, а для размерности 4 – в 1980-х гг. Случай с гомеоморфностью любой трехмерной поверхности трехмерной сфере оказался самым сложным. Показать это удалось лишь в 2002 г. петербургскому математику Григорию Перельману, который моментально прославился на весь мир. После серии неприятных интриг и попыток отобрать у него славу первооткрывателя Перельман, и без того имевший славу «сумасшедшего гения», порвал все контакты с официальным математическим миром, отказался от получения денежной премии от института Клэя и ведет затворнический образ жизни, не принимая многочисленные предложения о работе и участии во всевозможных профессиональных мероприятиях и форумах.

5. Гипотеза Ходжа
Область: алгебраическая геометрия
Сформулирована в 1941 г., остается нерешенной
Со времен Декарта алгебраическая геометрия достигла большого прогресса в описании форм сложных объектов. Мы можем предложить уравнение, решения которого будут соответствовать той или иной фигуре, например, сферу описать как (x — a)2 + (y — b)2 = r2. Если объект слишком сложен, мы можем аппроксимировать эту форму, «склеивая» вместе более простые фигуры – тогда ей будет соответствовать решение системы уравнений. Такой подход применяется очень широко, и математики далеко ушли даже от объектов, которым вообще соответствуют какие-либо геометрические аналоги – к тому, что называется более широким термином «многообразие».
Вопрос состоит в том, насколько этот подход можно применять к особому классу проективных алгебраических многообразий. Шотландец Уильям Ходж нашел остроумный метод, позволяющий проверять соответствие таких многообразий и алгебраические уравнения их представления, однако доказать его справедливость в общем случае пока не удается. Более того, математик Субит Чакрабарти считает эту задачу чересчур «абстрактной» для текущего уровня развития науки – ее решение требует разработки новых, плохо освоенных разделов алгебраической геометрии, и будет найдено очень нескоро. Пока что гипотеза доказана лишь для некоторых частных случаев, и математикам неизвестно, верна ли она в принципе.
6. Теория Янга – Миллса
Область: математическая физика (физика элементарных частиц)
Возникла в 1950-х, остается нерешенной
Теория Янга – Миллса относится к области физики элементарных частиц, являясь фундаментом современных представлений о них. По сути, это набор уравнений, которые пытаются предсказать поведение частиц и являются попыткой дать объединенное описание трех из четырех фундаментальных взаимодействий природы – сильного, слабого и электромагнитного. Удалось это лишь частично, создав аппарат для описания объединенного электрослабого взаимодействия. Решить уравнения, включив в них сильное взаимодействие, пока не получается, и для него найдено отдельное решение, которое, кстати, привело к открытию кварков.
Получается, что теория Янга – Миллса включает электрослабое взаимодействие и – отдельно – сильное. Эксперименты показывают, что она в принципе может их и объединить: предсказания уравнений согласуются с экспериментами, как натурными, так и расчетными, модельными. Однако математически доказать это пока не получается. Показано, что такая строгая теория требует построить описания для каждой компактной калибровочной группы – то есть группы преобразований, при которых свойства системы-частицы остаются неизменными (как сдвиг фазы не влияет на свойства волны-электрона), – причем сделать это предстоит для четырехмерного пространства-времени. Субит Чакрабарти предполагает, что решение этой задачи потребует около века и ювелирной работы нескольких поколений математиков.

7. Гипотеза Бёрча – Свиннертон-Дайера
Область: алгебраическая геометрия
Задача выдвинута в начале 1960-х, остается нерешенной
Уравнения, у которых и переменные, и решения являются целыми числами, названы в честь древнегреческого математика диофантовыми. В простейшем их виде они действительно просты – как, например, x2 = y: мы помним, что геометрическим решением такого школьного уравнения будет парабола. Но в более сложных случаях все становится по-настоящему сложным. Более того, еще советский математик Юрий Матиясевич показал, что универсального решения диофантовых уравнений не существует, тем самым ответив на вопрос 10-й проблемы Гильберта.
Гипотеза Бёрча — Свиннертон-Дайера (это два человека – Питер Свиннертон-Дайер и Брайан Бёрч) утверждает, что множество решений эллиптической кривой связано с поведением L-функции в районе 1. Эта функция вычисляется, как уже знакомая нам по гипотезе Римана дзета-функция, и количество рациональных решений бесконечно тогда (и только тогда), когда L(1) = 0. Математик Виктор Колывагин доказал в одну сторону, что если L(1) ≠ 0, то количество рациональных точек конечно. Проделать обратные выкладки не получается никак. По словам Субита Чакрабарти, возможно, что окончательное доказательство этой гипотезы в принципе не может быть получено, о чем говорит ответ на вопрос 10-й проблемы Гильберта. Вероятно, ответы на гипотезу Бёрча – Свиннертон-Дайера будут получены лишь в частном виде.
В той части Пиренеев, которые находятся на территории Испании, исследователи обнаружили первые доказательства добычи золота в эпоху Римской империи. На месте древних рудников нашли сложные гидравлические сооружения и остатки водохранилища, возраст которых определили с помощью метода оптического датирования. Открытие прольет свет на инженерные приемы римлян и поставит точку в многолетнем споре: действительно ли римляне добывали золото в этом регионе.
Ученые предложили новый способ оценки текущего темпа экспансии Вселенной с помощью едва уловимиого космического гравитационного «гула» от слияний неразличимых компактных объектов. Объединив данные наблюдений наземных интерферометров и статистику не выявленных сигналов, астрофизики получили уточненные ограничения параметра, вокруг которого разгорается один из самых острых споров в современной космологии.
Разное отношение домашних животных к хозяевам давно стало предметом споров, обсуждений и шуток. Ученые из Венгрии показали, что собаки демонстрируют по отношению к человеку уровень альтруизма, сходный с детским, тогда как кошки ищут в партнерстве с человеком прежде всего свою выгоду.
В той части Пиренеев, которые находятся на территории Испании, исследователи обнаружили первые доказательства добычи золота в эпоху Римской империи. На месте древних рудников нашли сложные гидравлические сооружения и остатки водохранилища, возраст которых определили с помощью метода оптического датирования. Открытие прольет свет на инженерные приемы римлян и поставит точку в многолетнем споре: действительно ли римляне добывали золото в этом регионе.
В мире оказалось гораздо больше диких пчел, чем кто-либо мог предположить. Ученые впервые оценили, сколько видов пчел существует на Земле, и обнаружили, что показатель превышает 26 тысяч — примерно на четверть больше, чем считалось.
Разное отношение домашних животных к хозяевам давно стало предметом споров, обсуждений и шуток. Ученые из Венгрии показали, что собаки демонстрируют по отношению к человеку уровень альтруизма, сходный с детским, тогда как кошки ищут в партнерстве с человеком прежде всего свою выгоду.
Астрономы недавно проанализировали базу данных о падающих на Землю объектах и пришли к выводу, что два из них прибыли из межзвездного пространства. Известна не только дата, но и место падения каждого из них.
«Любить лишь можно только раз», — писал поэт Сергей Есенин, а герои культовых сериалов приходили к выводу, что «настоящая» влюбленность случается в жизни максимум дважды. Однако ни один из этих тезисов не подкреплен научными данными. Американские исследователи подошли к вопросу иначе: опросили более 10 тысяч человек и вывели среднее число сильных влюбленностей, возможных в течение жизни.
В той части Пиренеев, которые находятся на территории Испании, исследователи обнаружили первые доказательства добычи золота в эпоху Римской империи. На месте древних рудников нашли сложные гидравлические сооружения и остатки водохранилища, возраст которых определили с помощью метода оптического датирования. Открытие прольет свет на инженерные приемы римлян и поставит точку в многолетнем споре: действительно ли римляне добывали золото в этом регионе.

Вы попытались написать запрещенную фразу или вас забанили за частые нарушения.
Понятно
Из-за нарушений правил сайта на ваш аккаунт были наложены ограничения. Если это ошибка, напишите нам.
Понятно
Наши фильтры обнаружили в ваших действиях признаки накрутки. Отдохните немного и вернитесь к нам позже.
Понятно
Мы скоро изучим заявку и свяжемся с Вами по указанной почте в случае положительного исхода. Спасибо за интерес к проекту.
Понятно







Последние комментарии