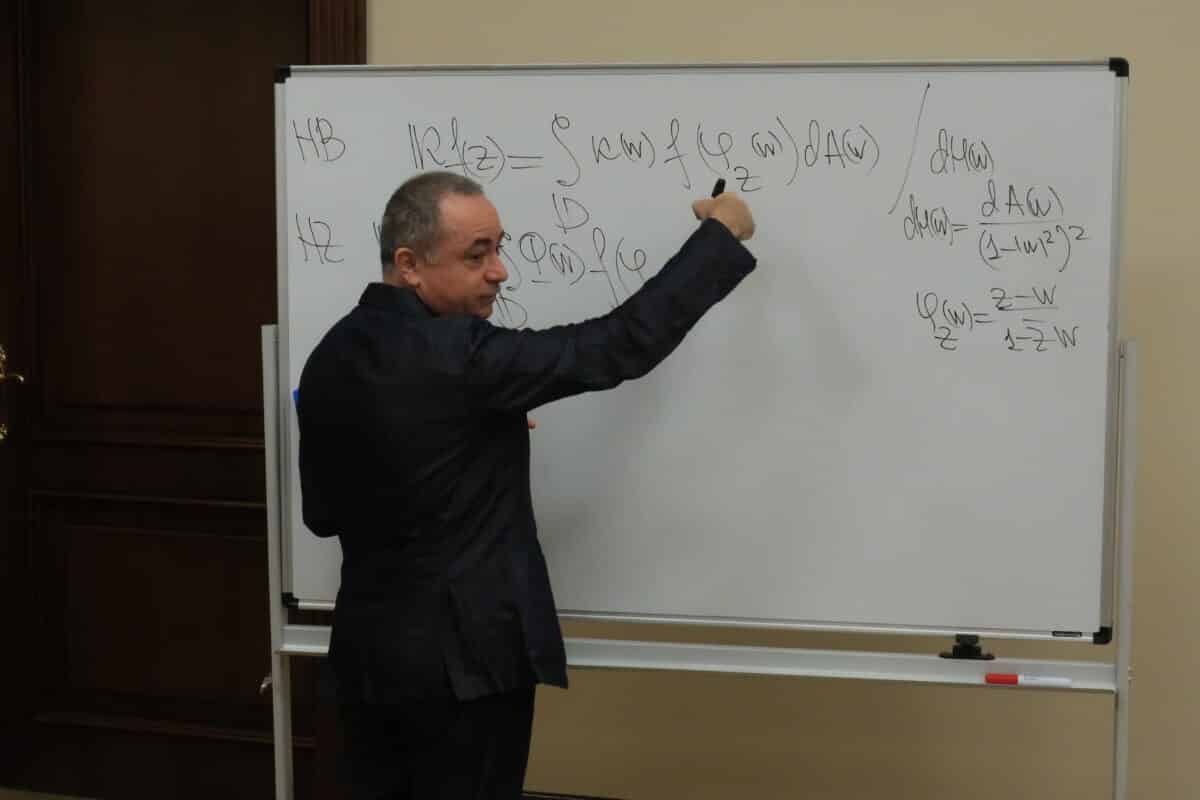Уведомления
Авторизуйтесь или зарегистрируйтесь, чтобы оценивать материалы, создавать записи и писать комментарии.
Авторизуясь, вы соглашаетесь с правилами пользования сайтом и даете согласие на обработку персональных данных.
В ЮФУ нашли новый подход к определению больших и малых пространств Лебега
Применение теории экстраполяции в определении больших и малых пространств Лебега открывает перспективы для новых направлений в математике. Ученые ЮФУ ожидают, что их исследование станет отправной точкой для развития новых теорий и методов в этой области, что поможет решать сложные проблемы с высокой точностью и эффективностью.
В математике, при решении реальных задач и построении математических моделей, функции играют ключевую роль. Известные нам со времен школы, они представляют собой не только абстрактные концепции, но и основу для описания физических процессов и явлений. Так, сегодня ученые используют в своих исследованиях совокупность таких функций, объединенных по некоторому признаку, которые в математике называют классами или пространствами функций. Для чего же это нужно? Функции могут описывать как начальные (исходные) условия, например температуру, скорость или положение объекта в начальный момент, так и само решение задачи, характеризующее конкретный физический процесс в зависимости от времени или от других параметров.
В обычной жизни мы привыкли работать с обычными числами, например, средней температурой или максимальной. Однако, иногда нам нужно уметь измерять глобальные характеристики объектов (функций), которые могут варьироваться по разным параметрам, например, по времени или по местоположению. Пространства Лебега как раз предоставляют инструменты для работы с такими сложными функциями: вместо того, чтобы просто смотреть на значения функции в конкретных точках, мы можем анализировать их в целом, учитывая их распределение, вариации и другие характеристики. Это особенно важно, например, при анализе физических процессов, которые описываются не в каждый момент времени, а некоторыми глобальными данными.
Интересно, что все функции, которые мы строили на графиках в школе, существуют в так называемом банаховом пространстве – нормированном векторном пространстве, полностью определенном нормой. В зависимости от области применения существуют разные подходы к тому, какие законы геометрии работают в этом пространстве: эвклидова геометрия, геометрия Лобачевского и так далее. При этом все функции, у которых интегрируется степень, существуют в Лебеговом пространстве. Однако работа с функциями в этом пространстве может быть сложной из-за его особых математических законов, поэтому математики давно пытаются упростить расчеты в нем.
В Южном федеральном университете над этой проблемой работает директор Регионального научно-образовательного центра ЮФУ Алексей Карапетянц. «В процессе построения математической модели зачастую приходят к интегральным уравнениям, в которых фигурируют эти самые функции. Но также часто оказывается, что геометрия исходного объекта не очень хороша для последующих приближенных вычислений, ввиду чего прибегают к искажению исходного пространства — замене координат.
При этом изучаемые объекты (области интегрирования) преобразуют в более подходящие для применения численных методов. Но это искажение пространства влечет за собой появление некоторого множителя в интеграле, отвечающего за это искажение, после чего вся подынтегральная конструкция может перестать быть интегрируемой из-за появления дополнительной особенности», – рассказал Алексей Карапетянц.
Ученый также отметил, что выходом было бы расширить исходное пространство функций так, чтобы после добавления этой особенности полученный объект продолжал бы оставаться в исходном классе функций, то есть быть интегрируемым. С другой стороны, расширение означает загрубление последующего результата, поэтому нужно обеспечить такое расширение, которое бы было больше исходного, но одновременно это расширение было бы практически «неуловимым».
Здесь в работу вступает так называемый «инфинитезимальный анализ», или анализ «бесконечно малых», некоторая философия математики, которая привычна для математиков уже много столетий, но в современном мире трактуется как что-то новое в приложениях и смежных областях наук.
Собственно, таким образом и появилось понятие «больших» пространств Лебега, которые больше самих классических пространств Лебега, но эта разница неуловима, если пытаться ее «измерить». Эти пространства функций возникли в работах Карло Сбордоне (Италия) и Тадеуша Иванеца (США/Польша) в начале 1990 годов. Однако предпосылки были получены в более ранних работах Николая Карапетянца и Бориса Рубина (РГУ, ныне-ЮФУ).
В новой работе, результаты которой опубликованы в журнале Mathematical Methods in the Applied Sciences, Алексей Карапетянц в соавторстве с математиком из Ярославля, партнером Математического Центра ЮФУ- Евгением Бережным, предлагает новую модель построения Больших пространств Лебега путем экстраполяции – хорошо знакомой математической операции.
«Наша работа является расширением уже классической теории на некоторые предельные показатели. Мы использовали новый в данном контексте метод, основанный на теории экстраполяции, то есть, когда математически «прогнозируются» свойства нового объекта на основе некоторого предельного перехода (экстраполирования). Данный подход позволяет проводить исследование в существенно более общей постановке, то есть обеспечивает унифицированную модель для широкого класс объектов», – объяснил ученый.
Ожидается, что это исследование откроет новые горизонты в теории больших и малых пространств Лебега, предоставляя математикам новые инструменты для анализа и решения сложных задач в различных областях науки и техники.
Telegram 
Дзен 
VK Арахнологи описали новый вид пауков, который копирует облик мертвой особи, пораженной паразитическим грибом, чтобы хищники меньше обращали на него внимание. В природе такой гриб заражает хозяина и воздействует на его нервную систему, после чего заставляет подниматься на возвышенность, откуда легче распространять споры. Открытие расширит представления ученых о мимикрии у животных.
Ученые из Центра исследований молекулярных механизмов старения и возрастных заболеваний МФТИ и Института биоорганической химии им. М. М. Шемякина и Ю. А. Овчинникова РАН с коллегами представили метод получения и очистки трансмембранного домена шиповидного белка коронавируса SARS-CoV-2 (SARStm) дикого типа. Этот «якорь» не только удерживает шип, которым вирус «атакует» клетки, в его оболочке, но и участвует в процессе слияния вирусной и клеточной оболочек. В новом протоколе используется бесклеточная экспрессия — синтез белка в очищенном бактериальном экстракте, что позволяет получать его в течение нескольких часов вместо дней и значительно упрощает очистку. Метод открывает возможность для детального изучения структуры белка с помощью спектроскопии ядерного магнитного резонанса (ЯМР).
Нанопластика становится все больше в диете среднего человека, но ученые ищут способы не дать ему переместиться из еды в организм навсегда. Оказалось, что источником защиты может стать квашеная капуста.
В парках некоторых стран все чаще можно заметить странную картину: синицы и воробьи вместо пуха и веточек приносят в клювах сигаретные окурки. Орнитологи из Польши решили выяснить, зачем птицы выстилают гнезда мусором, пропитанным никотином. Оказалось, пернатые нашли способ использовать вредную человеческую привычку для защиты своего потомства. Но, как это часто бывает в природе, у медали есть обратная сторона.
Арахнологи описали новый вид пауков, который копирует облик мертвой особи, пораженной паразитическим грибом, чтобы хищники меньше обращали на него внимание. В природе такой гриб заражает хозяина и воздействует на его нервную систему, после чего заставляет подниматься на возвышенность, откуда легче распространять споры. Открытие расширит представления ученых о мимикрии у животных.
20 марта Московскому авиационному институту исполняется 96 лет. За эти годы университет прошел большой путь становления, и во многом его развитие определяли люди, посвятившие себя науке и подготовке инженерных кадров. Один из таких — выдающийся ученый, заслуженный работник высшей школы Российской Федерации, доктор технических наук, профессор Борис Семенович Зечихин. Более 70 лет его жизнь неразрывно связана с кафедрой 310 «Электроэнергетические, электромеханические и биотехнические системы» и НИО-310 МАИ. Научная и педагогическая работа Бориса Семеновича получила широкое признание в России и за рубежом, а его вклад в развитие электромеханических специальностей и подготовку инженерных кадров оказал существенное влияние на отечественную авиационную и электротехническую промышленность. Сегодня Борис Семенович продолжает свою работу, участвует в проектах по созданию электрических и гибридных силовых установок, передает опыт и знания молодым специалистам в рамках развития Передовой инженерной школы и всего МАИ в целом.
В парках некоторых стран все чаще можно заметить странную картину: синицы и воробьи вместо пуха и веточек приносят в клювах сигаретные окурки. Орнитологи из Польши решили выяснить, зачем птицы выстилают гнезда мусором, пропитанным никотином. Оказалось, пернатые нашли способ использовать вредную человеческую привычку для защиты своего потомства. Но, как это часто бывает в природе, у медали есть обратная сторона.
Марсоход «Персеверанс» обнаружил в камнях на кромке кратера Езеро спектральные признаки минерала корунда, из которого на Земле образуются рубины и сапфиры. Такие спектры на Красной планете зарегистрировали впервые. Теперь ученые пытаются понять, при каких процессах он мог там сформироваться, ведь условия на Марсе заметно отличаются от тех, в которых корунд обычно образуется на Земле.
За 10 лет лежания в почве сигаретные фильтры не растворились, а лишь замаскировались под грязь. Их пластиковые волокна распались на микрочастицы, намертво склеились с минералами и превратились во вторичный микропластик. Более того, на пятом году гниения мусор начал отравлять землю с новой силой.
Вы попытались написать запрещенную фразу или вас забанили за частые нарушения.
Понятно
Из-за нарушений правил сайта на ваш аккаунт были наложены ограничения. Если это ошибка, напишите нам.
Понятно
Наши фильтры обнаружили в ваших действиях признаки накрутки. Отдохните немного и вернитесь к нам позже.
Понятно
Мы скоро изучим заявку и свяжемся с Вами по указанной почте в случае положительного исхода. Спасибо за интерес к проекту.
Понятно