Разработку представили немецкие ученые из Свободного университета Берлина (Freie Universität Berlin). Особенности разработки и обучения глубинной нейронной сети PauliNet они описали в статье, которая была опубликована в рецензируемом журнале Nature Chemistry. Поскольку материал доступен только по подписке, его основные тезисы также можно изучить в препринте, размещенном на портале arXiv годом ранее. С тех пор научная работа была существенно дополнена, в том числе практическими результатами, но общее представление о технологии дает и предварительная публикация.
Алгоритм PauliNet получил свое название в честь принципа Паули — одного из фундаментальных правил квантовой механики. Согласно этому принципу, два и более электрона в атомах не могут находиться в одинаковых квантовых состояниях. То есть при обмене электронами их волновая функция меняет знак. Эта антисимметрия, а также ряд других постулатов квантовой физики были «зашиты» в глубинную нейросеть (Deep neural network) сразу. А вот обучали ее уже другим свойствам элементарных частиц — в частности, сложным закономерностям распределения электронов по оболочкам вокруг ядер атомов.
На основе этих данных нейросеть научилась исследовать произвольные молекулы квантовыми методами Монте-Карло. Они подразумевают решение уравнений Шредингера для большого количества частиц. Основная сложность при выполнении таких задач — необходимость больших вычислительных мощностей для определения многочастичной волновой функции. Обычно используют более простые методы, например Теорию функционала плотности (DFT) или связанные кластеры (CC).
Однако такие упрощения создают ряд ограничений и для многих соединений все равно оказываются практически бесполезными. В результате физикам и химикам приходится постоянно искать компромиссы: или низкая точность, но относительно быстрые расчеты, либо высокая точность, но при этом нужно искать, на каком «железе» все это можно обсчитать. А в большинстве случаев выбора особого нет: сложные молекулы не по зубам даже современным суперкомпьютерам и системам распределенных вычислений.
А нейросети PauliNet удалось создать свою методику вычисления волновых функций. Этот алгоритм за вполне разумные сроки способен решать уравнения Шредингера для практически любых молекул.
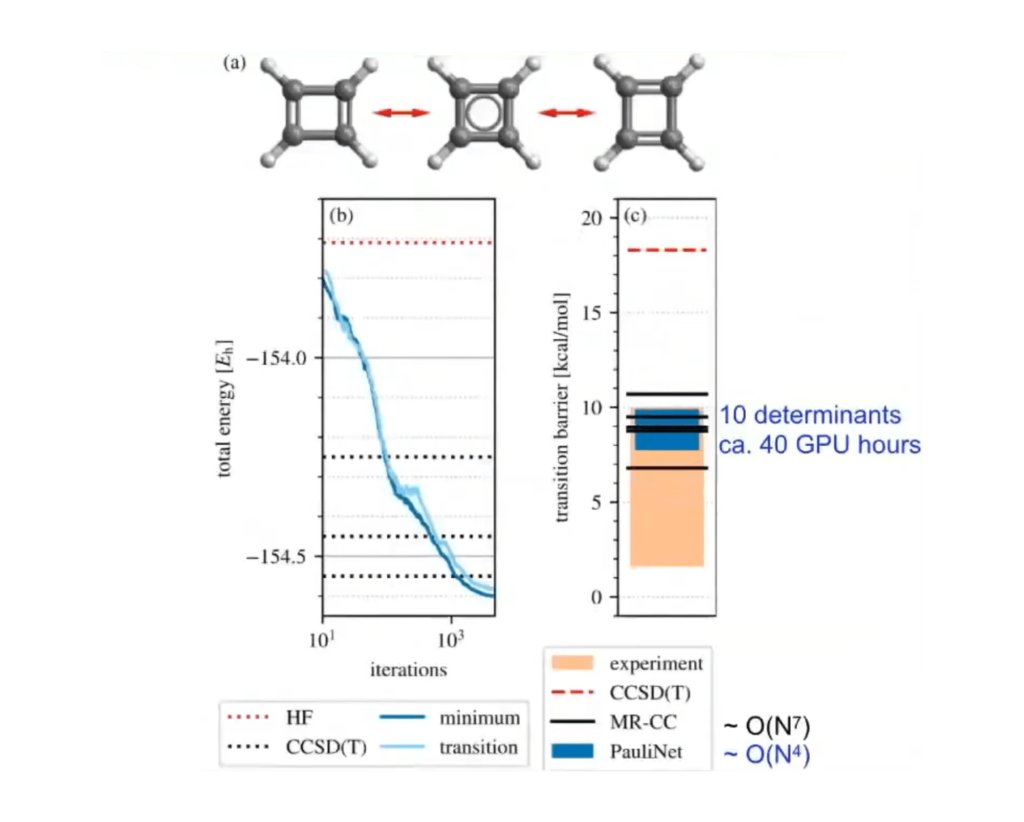
В приведенных примерах авторы этого искусственного интеллекта определяли свойства ряда соединений за считаные десятки часов работы обычных графических карт персональных компьютеров. Таким образом немецкие ученые нашли новый и чрезвычайно эффективный способ вычисления основного состояния произвольных молекул.