Исследователи из России вместе с их американским коллегой предложили новый, полностью децентрализованный алгоритм оптимизации. Он позволяет эффективно решать различные задачи, работая без центрального сервера и автоматически настраиваясь без предварительной настройки параметров.
Зависимость достигаемой точности от количества итераций для разных алгоритмов в задаче гребневой регрессии на разных графах: (1a) Линейный граф; (1b) Граф Эрдеша—Реньи с вероятностью активации ребра p = 0,1; (1c) Граф Эрдеша—Реньи с вероятностью активации ребра p = 0,5 / © NeurIPS 2024
Результаты исследования опубликованы в материалах конференции NeurIPS 2024. В современном мире множество задач решается в распределенных системах, где множество компьютеров (агентов) работают совместно. Традиционно такие системы используют центральный сервер для координации вычислений, что создает узкие места и проблемы с масштабируемостью.
Существующие децентрализованные алгоритмы оптимизации страдают от серьезного недостатка: для их эффективной работы необходимо точно знать параметры как самой задачи оптимизации (например, «константу Липшица» градиента, характеризующую крутизну функции потерь), так и топологии сети, по которой общаются агенты (степень их взаимосвязи). В реальных распределенных системах агенты обычно не имеют доступа к этой глобальной информации, что заставляет использовать очень консервативные настройки параметров и, как следствие, приводит к медленной сходимости или даже расходимости алгоритма. Это похоже на то, как если бы строители пытались построить дом, не зная ни плана здания, ни того, где находится строительный материал.
Однако новый подход, представленный в исследовании, решает эту проблему, предлагая полностью децентрализованный алгоритм оптимизации, работающий без центрального сервера и автоматически настраивающийся без необходимости в предварительной настройке параметров.
Он основан на методе «разбиения операторов» и использовании новой переменной метрики. Это позволяет каждому агенту самостоятельно определять оптимальный размер шага в процессе обучения, используя локальную информацию. Это подобно тому, как опытный строитель, оценивая ситуацию на месте, решает, какой инструмент и как использовать.
Вместо того, чтобы опираться на предварительно заданные параметры, алгоритм постоянно адаптируется к местным особенностям функции потерь. Каждый агент выполняет локальный поиск оптимального шага, не требуя обмена информацией со всеми остальными агентами в сети. Этот «локальный» подход значительно ускоряет вычисления и делает алгоритм более масштабируемым.
Теоретический анализ показал, что новый алгоритм обеспечивает линейную сходимость – это значит, что скорость приближения к решению остается высокой даже на поздних этапах вычислений. Скорость сходимости зависит от двух факторов: сложности самой задачи оптимизации и «связности» сети, то есть того, насколько хорошо агенты обмениваются информацией между собой. В хорошо связанных сетях скорость сходимости приближается к скорости централизованного алгоритма. Это как если бы все строители работали на одном участке, а не по всему городу.
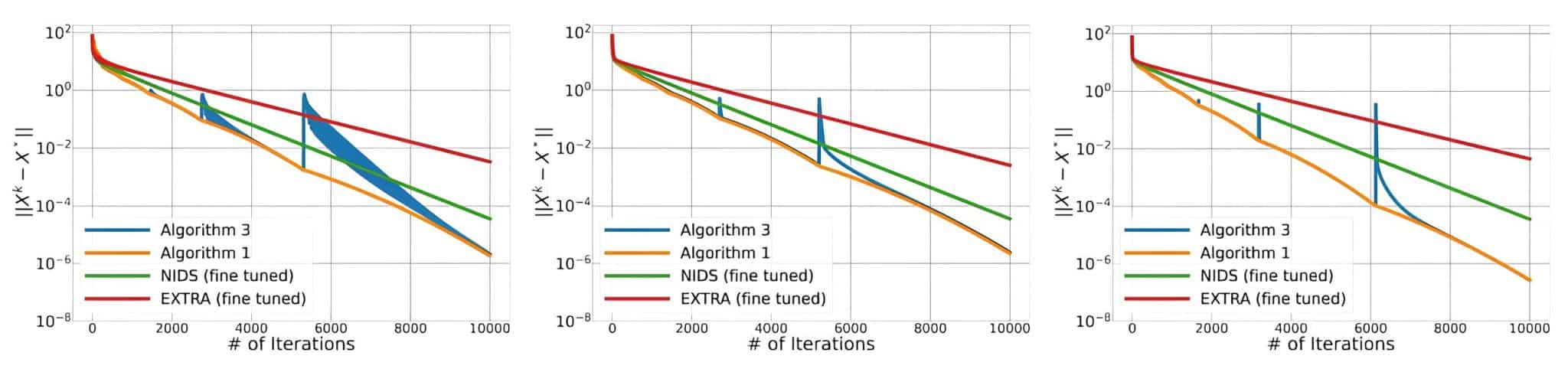
Авторы предложили две модификации своего алгоритма. Оба алгоритма являются децентрализованными и используют локальный линейный поиск для адаптивного выбора размера шага каждым агентом индивидуально. Однако механизм согласования этих локальных размеров шага различен. Первый алгоритм использует механизм поиска глобального минимума. Каждый агент вычисляет свой локальный оптимальный размер шага, а затем все агенты обмениваются этой информацией, и в качестве глобального размера шага выбирается минимальное значение среди всех агентов, что требует коммуникации между всеми агентами в сети. Второй алгоритм основан на использовании только локального минимума. Каждый агент вычисляет свой локальный оптимальный размер шага, а затем выбирает в качестве своего размера шага минимум среди своих непосредственных соседей, включая самого себя. Это требует коммуникации только с соседями в сети.
В итоге первый алгоритм обеспечивает более быструю сходимость за счет использования глобальной информации о размере шага, но требует большей коммуникации между агентами. Второй алгоритм, в свою очередь, менее требователен к коммуникации, обмениваясь информацией только с ближайшими соседями, но за счет этого может демонстрировать несколько более медленную сходимость (хотя авторы показывают, что разница не слишком велика). Выбор между алгоритмами зависит от компромисса между скоростью сходимости и объемом коммуникации в конкретной сети. Второй алгоритм особенно полезен для сетей с ограниченной пропускной способностью или высокой стоимостью коммуникации.
Численные эксперименты подтвердили теоретические выводы о том, что новые алгоритмы значительно превосходит по скорости существующие децентрализованные алгоритмы. Эта разница особенно заметна при решении сложных задач с большим количеством данных и при работе в слабо связанных сетях. Алгоритм был успешно протестирован на задаче гребневой регрессии (ridge regression) — распространенной задаче машинного обучения.
«Наш подход использует метод разбиения операторов с новой переменной метрикой, что позволяет использовать локальный поиск по линиям с обратным шагом (backtracking line-search) для адаптивного выбора размера шага без глобальной информации или обширной коммуникации, — рассказал Александр Гасников, заведующий лабораторией математических методов оптимизации МФТИ. — Это приводит к благоприятным гарантиям сходимости и зависимости от параметров оптимизации и сети по сравнению с существующими неадаптивными методами. Примечательно, что новый метод является первым адаптивным децентрализованным алгоритмом, который достигает линейной сходимости для сильно выпуклых и гладких функций».
Дальнейшие исследования ученых могут быть направлены на адаптацию предложенных методов к стохастических задачам, расширение его на более сложные типы сетевых топологий и обмен данными, исследование возможностей использования более сложных методов оптимизации в рамках предложенного подхода. Разработка и улучшение новых алгоритмов децентрализованного машинного обучения является важным шагом к созданию более эффективных и масштабируемых систем машинного обучения в распределенных средах.
