Одна из фундаментальных проблем при создании эффективных моделей машинного обучения — определение необходимого и достаточного количества данных для их обучения. Слишком мало данных — модель будет неточной, слишком много — неоправданные затраты времени и ресурсов на сбор и обработку информации. Ученые из МФТИ предложили два новых метода для решения этой задачи, основанных на анализе функции правдоподобия с использованием техники бутстрэпа.
Рисунок 1. Достаточный размер выборки по сравнению с порогом для трех наборов данных: синтетическая регрессия, синтетическая классификация и заболевания печени. По мере увеличения порогового значения ε достаточный размер выборки увеличивается. Это означает, что можно выбрать меньше объектов для удовлетворения желаемых значений предлагаемых функций D(k) и M(k) / © Computational Mathematics and Mathematical Physics
Работа опубликована в журнале Computational Mathematics and Mathematical Physics. Правдоподобием называют функцию, которая показывает, насколько вероятны наблюдаемые данные при заданных параметрах модели. В машинном обучении часто максимизируют эту функцию (или ее логарифм – логарифмическую функцию правдоподобия), чтобы найти наилучшие параметры модели.
Вопрос «сколько данных достаточно?» стар как само машинное обучение. От ответа на него напрямую зависит качество прогнозов модели, ее способность обобщать информацию и корректно работать на новых, ранее не просмотренных ею данных, а также экономическая целесообразность всего проекта.
Исторически сложилось несколько подходов к определению достаточного размера выборки. Во-первых, это классические статистические методы. Такие подходы часто опираются на проверку конкретных статистических гипотез о параметрах модели. Например, исследователи могут потребовать, чтобы модель достигала определенной статистической мощности (способности обнаружить эффект, если он есть) при заданном уровне ошибки первого рода (вероятности ложноположительного срабатывания). К таким методам относятся тест множителей Лагранжа, тест отношения правдоподобия, статистика Вальда. Основной их недостаток – они требуют сильных предположений о распределении данных и часто привязаны к конкретным гипотезам, что не всегда удобно на практике.
Во-вторых, это байесовские методы. В них размер выборки определяется, например, путем максимизации ожидаемой “полезности” модели, которая может учитывать как точность оценки параметров, так и штрафы за увеличение выборки. Используются различные критерии, такие как минимизация средней апостериорной дисперсии параметров, критерий среднего покрытия и другие. Эти методы гибки, но могут быть сложны в реализации и интерпретации, а также требуют задания априорных распределений для параметров модели, которые не всегда адекватно можно оценить.
В-третьих, используют множество эвристических методов, которые основаны на практическом опыте, эмпирических правилах (например, «10 объектов на каждую переменную») или методах вроде кросс-валидации (перекрестной проверки). Они просты, но не имеют строгого теоретического обоснования и не всегда гарантируют оптимальный результат.
Несмотря на разнообразие подходов, универсального, простого в применении и теоретически обоснованного метода для широкого класса задач до сих пор не существовало. Многие существующие техники либо сложны, либо требуют априорной информации, которой у исследователя может не быть на этапе планирования эксперимента. И все они не всегда гарантируют результат.
Именно проблему разработки более универсальных и практически применимых методов определения достаточного размера выборки решали исследователи из МФТИ. Их идея основана на интуитивном предположении: если данных уже достаточно, то добавление еще нескольких объектов не должно сильно менять ни саму модель, ни ее «уверенность» в данных, выраженную через функцию правдоподобия. Целью исследования ученых Физтеха была разработка критериев достаточности выборки, которые основаны на поведении функции правдоподобия при изменении размера обучающей подвыборки, и оценка их работоспособности в теории и на практике.
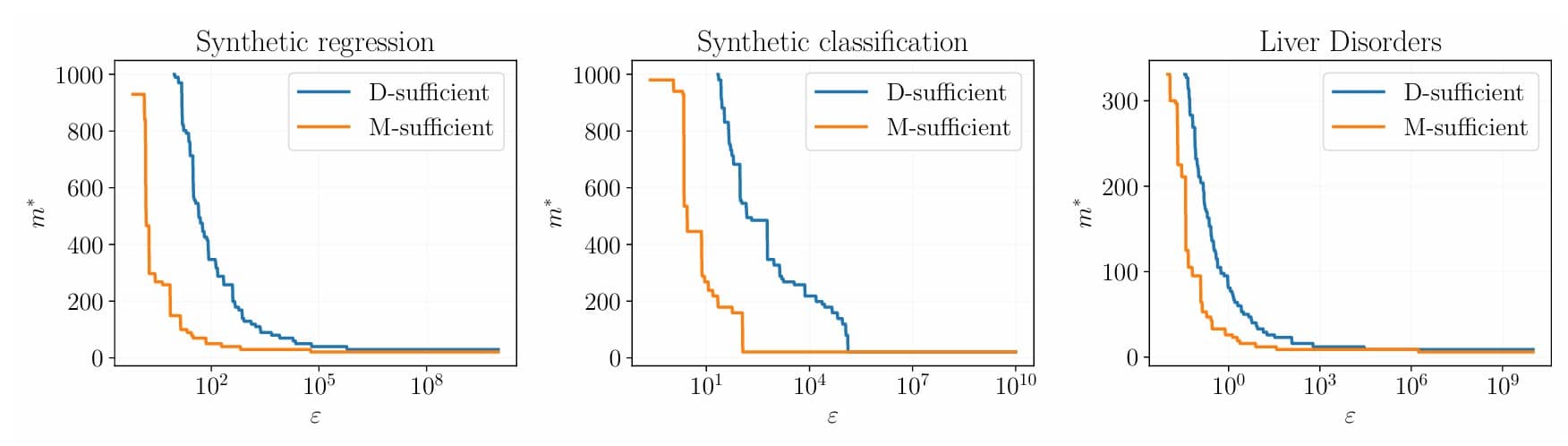
Авторы статьи предложили два критерия, основанных на анализе значений функции правдоподобия, вычисленной на подвыборках разного размера k, полученных с помощью бутстрэпа из исходной выборки некоторого размера m.
Первый критерий они назвали D-достаточностью, от слова “дисперсия”. Этот критерий проверяет, стабильны ли результаты при использовании разных подмножеств данных одного размера. Он заключается в том, чтобы считать выборку достаточной в том случае, если разброс значений правдоподобия между моделями, которые обучены на разных случайных подвыборках размера k, достаточно мал.
Второй критерий они назвали M-достаточностью, от «математическое ожидание». M-критерий проверяет, перестала ли модель существенно улучшаться при добавлении еще одного объекта данных. Если средний показатель правдоподобия при добавлении одного элемента данных почти не улучшился, то это значит, что выборка уже является достаточной.
Оба подхода используют бутстрэп для получения надежных оценок этой стабильности или улучшения. Бутстрэп — это статистический метод, позволяющий оценить различные характеристики некоторой статистики путем многократного извлечения подвыборок с возвращением из исходной выборки. Проще говоря, мы много раз «вытаскиваем наугад» объекты из нашего набора данных (причем один и тот же объект может быть выбран несколько раз в одну подвыборку), формируя множество «псевдо-выборок», и на них оцениваем интересующие нас величины.
Важным результатом работы является теоретическое доказательство корректности критерия M-достаточности для модели линейной регрессии при определенных условиях сходимости оценок параметров модели. Это придает методу дополнительную строгость, хотя бы для одного важного класса моделей.
Ученые провели вычислительные эксперименты как на синтетических данных (сгенерированных из моделей линейной и логистической регрессии), так и на реальных наборах данных (включая известный набор Liver Disorders и множество других).
Эмпирические результаты в виде численного моделирования использования метода подтвердили работоспособность обоих подходов. На практике оказалось, что предложенный подход можно эвристически применять даже в тех случаях, когда оптимизируется не функция правдоподобия, а некоторая другая функция потерь, что часто встречается в современном машинном обучении.
Эксперименты показали, что методы успешно применимы к разным типам данных и моделей (регрессия, классификация).
Хотя бутстрэп сам по себе известен, его применение для оценки именно стабильности правдоподобия как критерия достаточности выборки является новым. Предложенный учеными подход является универсальным, так как он не привязан к конкретным статистическим гипотезам и может быть применен к широкому кругу моделей, включая те, где оптимизируется произвольная функция потерь.
«Определение правильного объема данных — это вечный компромисс между затратами на сбор информации и качеством модели, – рассказал Андрей Грабовой, доцент кафедры интеллектуальных систем МФТИ. – Существующие методы часто либо слишком сложны в применении, либо опираются на специфические допущения о данных или модели, которые не всегда выполняются. Мы хотели предложить простой, но при этом имеющий под собой основания подход. Идея в том, чтобы посмотреть, насколько ‘устаканивается’ правдоподобие модели по мере добавления данных, используя для оценки этой стабильности бутстрэп. Наши эксперименты на синтетических и реальных данных показывают, что предложенные критерии D- и M-достаточности действительно сходятся к нулю при увеличении выборки, что подтверждает их адекватность. Мы надеемся, это поможет исследователям и практикам более уверенно планировать свои эксперименты и эффективнее использовать имеющиеся ресурсы».
Никита Киселев, студент 5-го курса МФТИ, добавил: «Наше исследование было вдохновлено эмпирическими наблюдениями: мы обнаружили, что в наших экспериментах функция правдоподобия переставала значимо изменяться при достижении определенного размера выборки. Это наблюдение побудило нас к глубокому теоретическому анализу проблемы, результаты которого представлены в данной статье. Наши выводы имеют широкое применение для различных моделей, хотя для современных нейронных сетей, включая генеративные модели, мы уже разработали более эффективные и выразительные методы, которые планируем подробно осветить в будущих работах».
Предложенные методы могут найти применение во множестве областей, где используется машинное обучение и остро стоит вопрос стоимости или возможности сбора данных. Такими являются, например, медицинские исследования, где крайне важно определить достаточное количество пациентов для клинических испытаний новых лекарств; финансовый анализ, для которого необходима оценка достаточного объема исторических данных для построения моделей кредитного скоринга, прогнозирования рынков или обнаружения мошенничества. Также предложенные методы могут иметь применения в обработке данных в социологии, маркетинге, промышленности, биоинформатике, в разработке систем искусственного интеллекта.
Работа ученых из МФТИ открывает несколько направлений для будущих исследований. Это и более углубленный теоретический анализ предложенных методов с целью строго доказать их корректность, и использование других метрик стабильности, разработка других похожих алгоритмов, сравнение с другими методами, исследование влияния гиперпараметров – как на эффективность метода влияют выбор порога ε и число используемых подвыборок для бутстрэпа.
