Исследователи из Международной лаборатории динамических систем и приложений НИУ ВШЭ — Нижний Новгород разработали теорию, которая позволяет с математической точностью доказать существование устойчивого хаотичного поведения в сетях взаимодействующих элементов. Работа открывает новые возможности для изучения сложных динамических процессов в нейронауке, биологии, медицине, химии, оптике и других областях.
Псевдогиперболический аттрактор / © E. Karatetskaia
Результаты исследования приняты к публикации в ведущем международном научном журнале Physical Review Letters. С результатами исследования можно ознакомиться в архиве Arxiv.org.
В научной терминологии хаос означает не беспорядок, а динамику, которая отличается крайней чувствительностью к малейшим изменениям. В таких режимах поведение системы становится непредсказуемым, что в ряде случаев оказывается полезным. Например, в нейронауке устойчивый хаос помогает предотвратить чрезмерную синхронизацию нейронов и, как следствие, эпилептические приступы. В алгоритмах искусственного интеллекта хаотические режимы способствуют повышению эффективности обучения.
Хаотическая динамика также используется для описания поведенческих и экономических циклов и помогает строить более точные краткосрочные прогнозы. Однако до последнего времени оставался открытым вопрос: как понять, является ли наблюдаемая динамика действительно хаотической, или это лишь временное явление, за которым последует стабилизация системы?
Ученые НИУ ВШЭ — Нижний Новгород, профессор Алексей Казаков и аспиранты Ефросиния Каратецкая и Клим Сафонов, совместно с профессором Имперского колледжа Лондона Дмитрием Тураевым смогли дать ответ на этот вопрос, применив концепцию псевдогиперболичности.
Профессор Тураев принимал участие в создании этой концепции вместе с нижегородским математиком Леонидом Шильниковым. Это свойство системы исключает переход к устойчивому состоянию и гарантирует сохранение хаотического поведения, даже если на систему действуют малые внешние возмущения. С помощью проверки условий псевдогиперболичности исследователи доказали, что сети из четырех и более идентичных взаимодействующих осцилляторов могут демонстрировать устойчивый хаос при определенных функциях связей между элементами.
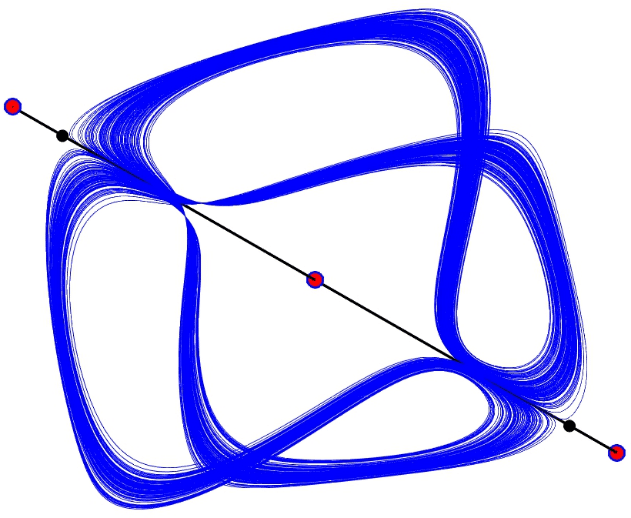
Более того, авторы построили численные карты областей существования устойчивого и неустойчивого хаоса и описали разные типы хаотических аттракторов, включая двукрылые и четырехкрылые аналоги классического аттрактора Лоренца.
Исследование реализовано в рамках проекта «Центры превосходства НИУ ВШЭ», а также Межкампусного проекта Программы фундаментальных исследований НИУ ВШЭ.
