Работа поддержана грантом Российского научного фонда и опубликована в журнале Computational Mathematics and Mathematical Physics.
Одним из главных инструментов современной геофизики является сейсморазведка. Инициировав на поверхности упругое возмущение, например, небольшой контролируемый взрыв, ученые с помощью сети датчиков слушают «эхо» Земли — отраженные и рассеянные сейсмические волны. Анализируя время их прихода и форму, можно, как по УЗИ, построить карту подземных структур: геологических слоев, разломов или месторождений нефти и газа. Однако точность такой карты напрямую зависит от качества компьютерных моделей, способных предсказать, как именно волны будут путешествовать сквозь слоистую и неоднородную толщу земной коры.
Создание таких моделей — чрезвычайно сложная вычислительная задача. Главный вызов — это сложная геометрия. Границы между геологическими слоями редко бывают плоскими; они изгибаются, обрываются, образуя причудливый рельеф. Чтобы описать такую структуру в компьютере, ее необходимо разбить на элементарные ячейки — создать расчетную сетку. Существующие численные методы здесь сталкиваются с дилеммой. С одной стороны, есть быстрые и эффективные методы, например, сеточно-характеристический, которые прекрасно работают на простых, регулярных сетках, похожих на миллиметровую бумагу. Но такой сеткой невозможно точно «обернуть» искривленную поверхность. С другой стороны, существуют гибкие подходы, такие как разрывный метод Галеркина, которые используют неструктурированные сетки из элементов произвольной формы, например, тетраэдров. Они идеально подходят для описания сложной геометрии, но их применение ко всей расчетной области требует колоссальных вычислительных ресурсов.
Исследователи поставили перед собой задачу создать решение, которое бы объединило лучшее из двух миров: скорость и эффективность регулярных сеток с геометрической гибкостью неструктурированных. Они разработали гибридный алгоритм, который делит всю область моделирования на две части. Основной объем геологической среды, где границы слоев достаточно просты, описывается с помощью быстрого сеточно-характеристического метода на регулярной структурированной сетке. А те области, где находятся сложные искривленные границы, покрываются локальной сеткой из тетраэдров, для которой применяется более сложный, но геометрически точный метод прерывных Галеркина.
Алена Фаворская, ведущий научный сотрудник лаборатории прикладной вычислительной геофизики МФТИ, пояснила: «Наш подход можно сравнить с пошивом сложного костюма. Для больших и простых частей, таких как спина или рукава, портной использует простой и быстрый шов на стандартном куске ткани. Но для воротника или манжет сложной формы требуется кропотливая ручная работа и фигурный крой. Мы поступили так же с нашей вычислительной моделью. Основной объем «шьется» быстрым методом на простой сетке, а «воротники» — то есть сложные геологические границы — мы аккуратно «обшиваем» гибкой тетраэдральной сеткой. Самое сложное и интересное в нашей работе было разработать математически корректный «стежок» — алгоритм, который бы безупречно соединял эти два разных мира, обеспечивая бесшовный обмен информацией на границе между сетками без потери точности. Такие гибридные численные методы являются актуальным направлением исследований для научных групп из разных стран в последние годы».
Новизна работы заключается в создании и тщательной верификации такого трехмерного «бесшовного стежка». Ученые разработали специальные алгоритмы для вычисления потоков физических величин на границе между двумя областями, что позволило методам корректно обмениваться данными на каждом шаге расчета.
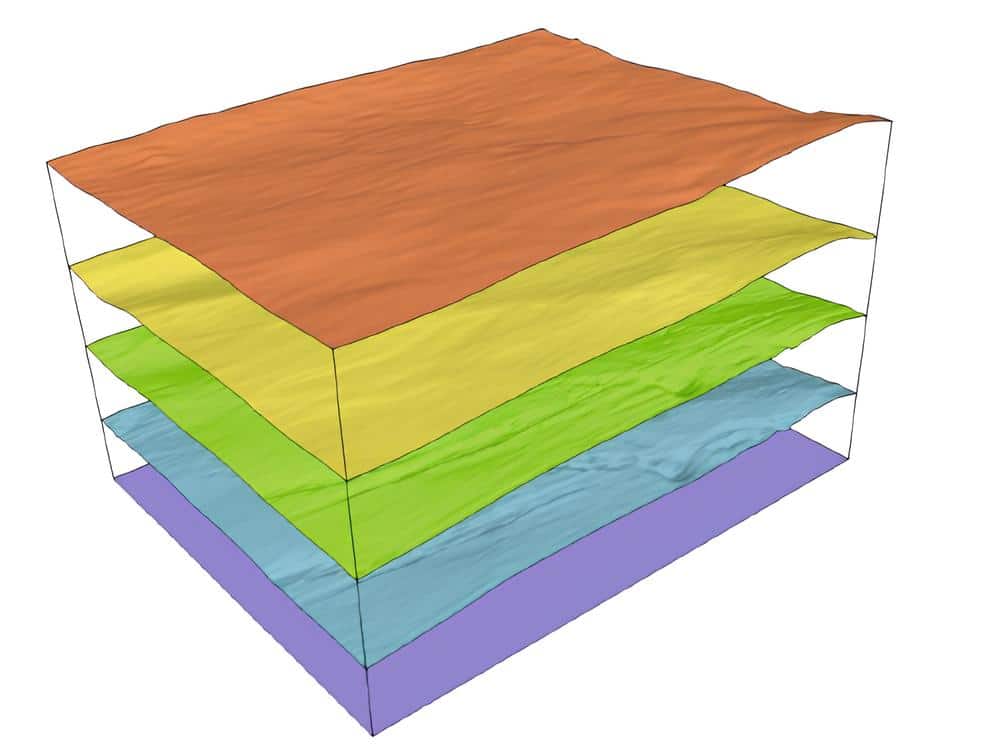
Чтобы доказать эффективность своего подхода, команда провела серию численных экспериментов. Они смоделировали распространение сейсмической волны от точечного источника в среде, состоящей из четырех слоев с искривленными границами. Затем они сравнили результаты работы нового гибридного метода с результатами, полученными с помощью традиционного, но более ресурсоемкого подхода, где вся область описывалась единой, пусть и сложной, криволинейной сеткой.
Оказалось, что гибридный метод продемонстрировал более высокий порядок сходимости, то есть его точность растет быстрее при уменьшении размера ячеек сетки. Кроме того, сравнительный анализ показал значительное преимущество в эффективности. При увеличении детализации модели, когда количество расчетных узлов возрастает, гибридный метод оказывается экономичнее по использованию памяти и времени, поскольку ресурсоемкий метод Галеркина применяется лишь на малой части всей области.
Разработанный алгоритм полезен для более точного и быстрого моделирования в целях сейсморазведки месторождений углеводородов и других полезных ископаемых. Он также может быть применен для решения широкого круга других научных и инженерных задач, где необходимо моделировать волновые процессы в объектах сложной геометрии — от анализа сейсмической опасности до ультразвукового контроля промышленных изделий.