Российские исследователи из МФТИ, МИСИС и Российского квантового центра предложили новое семейство кодов квантовой коррекции ошибок, отличающихся низкими ресурсными затратами и специально адаптированных для кольцевой архитектуры квантовых процессоров, в частности, на основе сверхпроводниковых кубитов. Кроме того, они разработали и продемонстрировали эффективность инновационного декодера на основе нейронных сетей для исправления ошибок в этих кодах.
Рисунок 1. Схематическое изображение 13-кубитного кода на кольцевой топологии и часть квантовой схемы. Красные и аквамариновые круги обозначают информационные и вспомогательные кубиты соответственно. Полную квантовую схему можно реконструировать, транслируя показанный сегмент. Основная часть схемы — это шесть серий двухкубитных гейтов, применяемых к соседним кубитам. Мы выделяем путь вычислительного состояния первого вспомогательного кубита и показываем кубиты данных, с которыми он взаимодействует во время цикла коррекции. Мы также подчеркиваем, что вычислительные состояния кубитов данных сдвигаются в конце цикла / © Илья Симаков, Илья Беседин, Physical Review A
Работа опубликована в журнале Physical Review A. Квантовые компьютеры обещают революцию во многих областях, от разработки лекарств и материалов до криптографии и искусственного интеллекта, благодаря своей способности выполнять вычисления, недоступные классическим суперкомпьютерам. Их строительным блоком является кубит – квантовый бит. В отличие от классического бита (0 или 1), кубит может находиться в суперпозиции (одновременно и 0, и 1) и быть запутанным с другими кубитами, что и дает квантовым компьютерам преимущество над классическими компьютерами. Но эта же квантовая природа делает кубиты чрезвычайно чувствительными к внешним воздействиям – шуму, температуре, электромагнитным полям.
Взаимодействие с окружением неизбежно приводит к ошибкам – случайным изменениям состояния кубитов. Современные квантовые процессоры имеют частоту ошибок порядка 1 на 1000 операций (10⁻³), что катастрофически много для сложных вычислений. Без надежной защиты от ошибок построить полномасштабный квантовый компьютер невозможно.
Решением этой проблемы является квантовая коррекция ошибок. Ее основная идея, заимствованная из классической теории кодирования, заключается в том, чтобы кодировать информацию одного «идеального» логического кубита с помощью множества реальных, «шумных» физических кубитов. Эти физические кубиты находятся в сложном запутанном состоянии. Специальные измерительные процедуры позволяют обнаруживать ошибки, возникающие в отдельных физических кубитах, и исправлять их, не разрушая при этом хрупкую квантовую информацию.
Одним из наиболее перспективных подходов к квантовой коррекции ошибок являются стабилизаторные коды. В таких кодах логическое состояние определяется как общее состояние, которое не изменяется под действием определенного набора квантовых операторов – стабилизаторов. Измеряя эти стабилизаторы (точнее, их собственные значения +1 или -1), получают синдром ошибки – набор битов, указывающий, произошла ли ошибка и, возможно, где именно. Самое главное здесь заключается в том, что измерение синдрома не «спрашивает» у системы, в каком логическом состоянии она находится, а лишь проверяет, не нарушены ли «правила» кода.
Для исправления ошибки уже нужен декодер – алгоритм, который по измеренному синдрому определяет наиболее вероятную произошедшую ошибку и вычисляет необходимую корректирующую операцию.
Любой квантовый код коррекции ошибок характеризуется расстоянием кода (мерой способность исправлять ошибки), затратами ресурсов и топологией (схемой взаимодействия кубитов, которая необходима для работы стабилизаторов).
Многие известные коды, такие как поверхностный код («surface code») или цветной код («color code»), демонстрируют хорошие свойства масштабирования (ошибка логического кубита уменьшается экспоненциально с ростом расстояния кода), но требуют большого числа кубитов (квадратично растущего с расстоянием кода) и имеют специфическую двумерную решетчатую топологию.
Самым маленьким кодом, способным исправить любую одиночную ошибку, является пятикубитный совершенный код. Интересно, что его стабилизаторы можно получить циклической перестановкой одного базового стабилизатора. Это наводит на мысль о кодах с циклической структурой.
Перед авторами исследования стояла задача разработать новые коды квантовой коррекции ошибок, которые бы обладали низкими ресурсными затратами, особенно по числу кубитов, чтобы их можно было реализовать на существующих и ближайшего будущего квантовых процессорах (несколько десятков кубитов). Кроме того, такие коды должны быть совместимы с реалистичной топологией сверхпроводниковых чипов, в частности, с кольцевой архитектурой, где кубиты расположены по кругу и взаимодействуют с соседями. Они должны иметь эффективный декодер для исправления ошибок и допускать возможность масштабирования (увеличения расстояния кода для лучшей защиты при сохранении разумных затрат ресурсов).
Ученые предложили семейство кодов, основанных на идее циклического сдвига базового стабилизатора, подобно пятикубитному коду, но для больших расстояний (d=3, 5, 7, 9). Все остальные стабилизаторы кода получаются циклическим сдвигом индексов кубитов в базовом стабилизаторе.
Число физических кубитов n, необходимых для кодирования одного логического кубита таким кодом коррекции ошибок, растет линейно с расстоянием кода. Это значительно эффективнее квадратичного роста у поверхностных или цветовых кодов, особенно для малых и средних расстояний кода. Однако, есть и обратная сторона: вес стабилизаторов (число нетождественных квантовых операторов в них) растет с увеличением расстояния кода, что усложняет их измерение и декодирование.
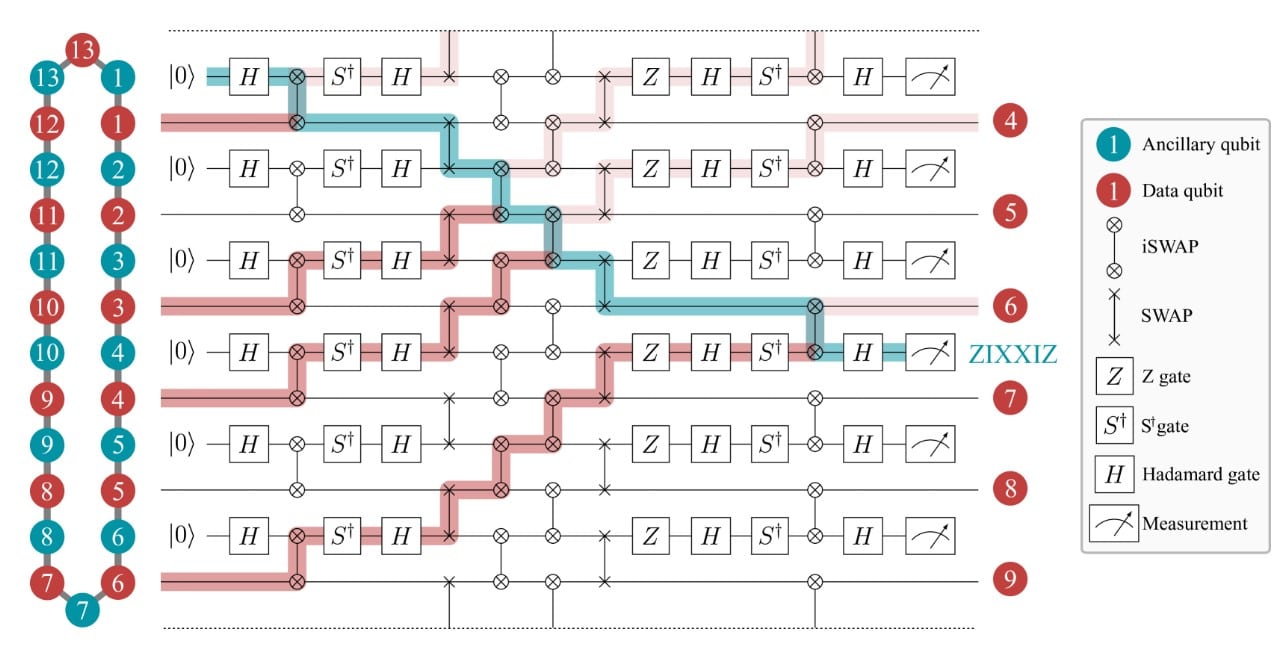
Российские ученые разработали квантовую схему для реализации этих кодов на кольце из 2n физических кубитов. В этом кольце чередуются n кубитов данных (хранящих логическую информацию) и n вспомогательных кубитов (анцилл), используемых для измерения синдромов. Схема использует только двухкубитные операции обмена iSWAP и SWAP между соседними кубитами, что типично для сверхпроводниковых платформ. iSWAP гейт в отличие от SWAP гейт не только обменивает состояния двух кубитов, но и добавляет так называемый фазовый сдвиг.
Операция CNOT («Controlled NOT») – это квантовая операция, которая позволяет создавать запутанные состояния между двумя кубитами. Она действует следующим образом: если первый кубит находится в состоянии 1, то второй меняет свое состояние. Если же первый кубит находится в состоянии 0, то изменений не происходит. Эта операция является основой для многих квантовых протоколов
Чтобы анцилла могла взаимодействовать с несколькими кубитами данных, которые не являются ее прямыми соседями, авторы применили элегантный трюк. Комбинация стандартных CNOT и SWAP- гейтов (для перемещения анциллы) эффективно заменяется одной или несколькими операциями iSWAP и однокубитными вращениями. В ходе цикла коррекции анциллы и кубиты данных как бы «скользят» в противоположных направлениях по кольцу, позволяя каждой анцилле «собрать» информацию о состоянии нужных ей кубитов данных.
Для тестирования кода в работе использовалась феноменологическая модель ошибок. Она заключается в том, что на кубитах данных между циклами коррекции с вероятностью p могут произойти случайные ошибки X, Y или Z (с равной вероятностью p/3), а на вспомогательных кубитах непосредственно перед измерением с вероятностью q (в симуляции q=p) может произойти ошибка типа X, искажающая результат измерения синдрома. Эти ошибки не портят логический кубит напрямую, но сильно усложняют декодирование.
Декодирование кодов с высоким весом стабилизаторов и смешанными ошибками X/Z является очень сложной задачей, для которой далеко не всегда подходят стандартные методы. Авторы предложили использовать рекуррентную нейронную сеть (RNN), а именно архитектуру LSTM («Long Short-Term Memory»), которая хорошо подходит для анализа последовательностей данных во времени (синдромы измеряются циклически).
Главная научная новизна здесь заключается в гибридном подходе. Вместо того, чтобы подавать на вход нейросети только «сырые» данные об изменениях синдромов («детекторы»), авторы добавили предобработку с помощью простого, но модифицированного декодера на основе таблицы поиска.
Стандартные таблицы поиска просто сопоставляют наблюдаемый синдром наиболее вероятной ошибке. Авторы улучшили этот алгоритм, введя «глубину памяти» (D). Если в текущем цикле k обнаружен ненулевой синдром, декодер «смотрит вперед» на D следующих циклов. Если там ошибок нет, он применяет коррекцию по таблице поиска в цикле k. Если же в следующих D циклах тоже есть ошибки (что может быть признаком ошибки измерения), он «откладывает» коррекцию, добавляя синдром цикла k к синдрому следующего цикла k+1. Это помогает бороться с ошибками измерения.
Нейросеть обучалась на данных, включающих сырые детекторы ошибок, предсказания таблиц поиска с D = 1 (с минимальной памятью) и предсказания таблиц поиска с D = 2). Идея здесь заключается в том, что таблицы поиска быстро «подсказывают» сети возможные простые сценарии, а сеть учится распознавать более сложные паттерны и комбинировать полученную информацию.
Ученые провели симуляцию работы предложенных циклических кодов (d=3, 5, 7, 9) в режиме «квантовой памяти» (сохранение начального состояния) на протяжении до 50 циклов коррекции. Моделирование показало, что логическая частота ошибок (ϵ) – вероятность ошибки на логическом кубите после коррекции – уменьшается экспоненциально с ростом физической частоты ошибок p в соответствии с ожидаемым законом. Это подтверждает, что коды действительно обладают заявленным расстоянием d и способны эффективно подавлять ошибки в рамках использованной модели. Сравнение различных декодеров для кода d=7 показало, что гибридный LSTM-декодер, использующий предобработку с помощью таблиц поиска с глубиной памяти 1 и с глубиной памяти 2, демонстрирует наилучшую производительность, превосходя как отдельные декодеры на основе таблицы поиска, так и нейросеть, обученную только на сырых данных.
Илья Симаков, аспирант Физтех-школы физики и исследований имени Ландау МФТИ, рассказал: «Создание практически полезного квантового компьютера — это марафон, и квантовая коррекция ошибок — необходимый этап на этом пути. В нашей работе рассмотрена проблема коррекции ошибок на квантовых процессорах с ограниченной связностью и предложен подход, позволяющий одновременно запутывать кубиты и обменивать их состояния, тем самым эффективно перенаправляя физические кубиты.
Такой метод снижает требования к числу физических кубитов и элементов связи по сравнению с традиционными схемами и открывает новые возможности для реализации кодов коррекции на процессорах с ограниченной связностью. Особая гордость – наш гибридный декодер, где мы научили нейросеть эффективно использовать ‘подсказки’ от более простых алгоритмов, что позволило ей лучше справляться со сложными комбинациями ошибок. Демонстрация экспоненциального подавления ошибок в симуляциях подтверждает перспективность такого подхода».
Ученые отмечают, что в последующих исследованиях необходимо рассмотреть производительность кодов и декодера в условиях более сложных, аппаратно-зависимых моделей шума (например, «circuit-level noise»), которые включают коррелированные ошибки от двухкубитных гейтов (т.н. «hook errors»). Авторы предполагают, что добавление «флаговых» кубитов в схему может помочь справиться с такими ошибками. Главный следующий шаг – экспериментальная проверка предложенных кодов и декодера на реальном квантовом процессоре с кольцевой топологией. Это позволит оценить реальную производительность и выявить доминирующие каналы ошибок, связанные с операцией iSWAP. Затем необходимо дальнейшее улучшение гибридного декодера, возможно, с использованием других архитектур нейронных сетей или более сложных методов предобработки.
Проделанная работа представляет собой важный вклад, предлагая прагматичный и ресурсоэффективный подход и приближая нас к эре квантовых технологий, защищенных от ошибок.
Исследование поддержано Российским научным фондом и Министерством науки и высшего образования РФ в рамках программы стратегического академического лидерства «Приоритет 2030» (стратегический проект «Квантовый интернет»).
