Результаты исследования, меняющие взгляд на структуру реальности на самом глубоком уровне, опубликованы в «Журнале экспериментальной и теоретической физики» (ЖЭТФ).
Общая теория относительности Эйнштейна описывает гравитацию как проявление кривизны пространства-времени, которое представляется гладким и непрерывным, подобно натянутому резиновому листу. Однако для расчетов, особенно в области квантовой гравитации, физики часто используют приближенный метод, известный как исчисление Редже. Этот подход, предложенный еще в 1961 году, предлагает рассматривать искривленное пространство как мозаику, склеенную из множества маленьких плоских «кусочков» — симплексов. В такой «скелетной» геометрии вся кривизна концентрируется не в объеме, а на «швах» и «стыках» этой мозаики. Эти стыки, где сходятся несколько плоских фрагментов, и есть конические сингулярности. Простейший пример такой сингулярности — вершина обычного бумажного конуса. Если вырезать из листа бумаги сектор и склеить края, в центре образуется точка, где кривизна бесконечна. Угол вырезанного сектора, так называемый дефицит угла, и будет мерой этой сконцентрированной кривизны.
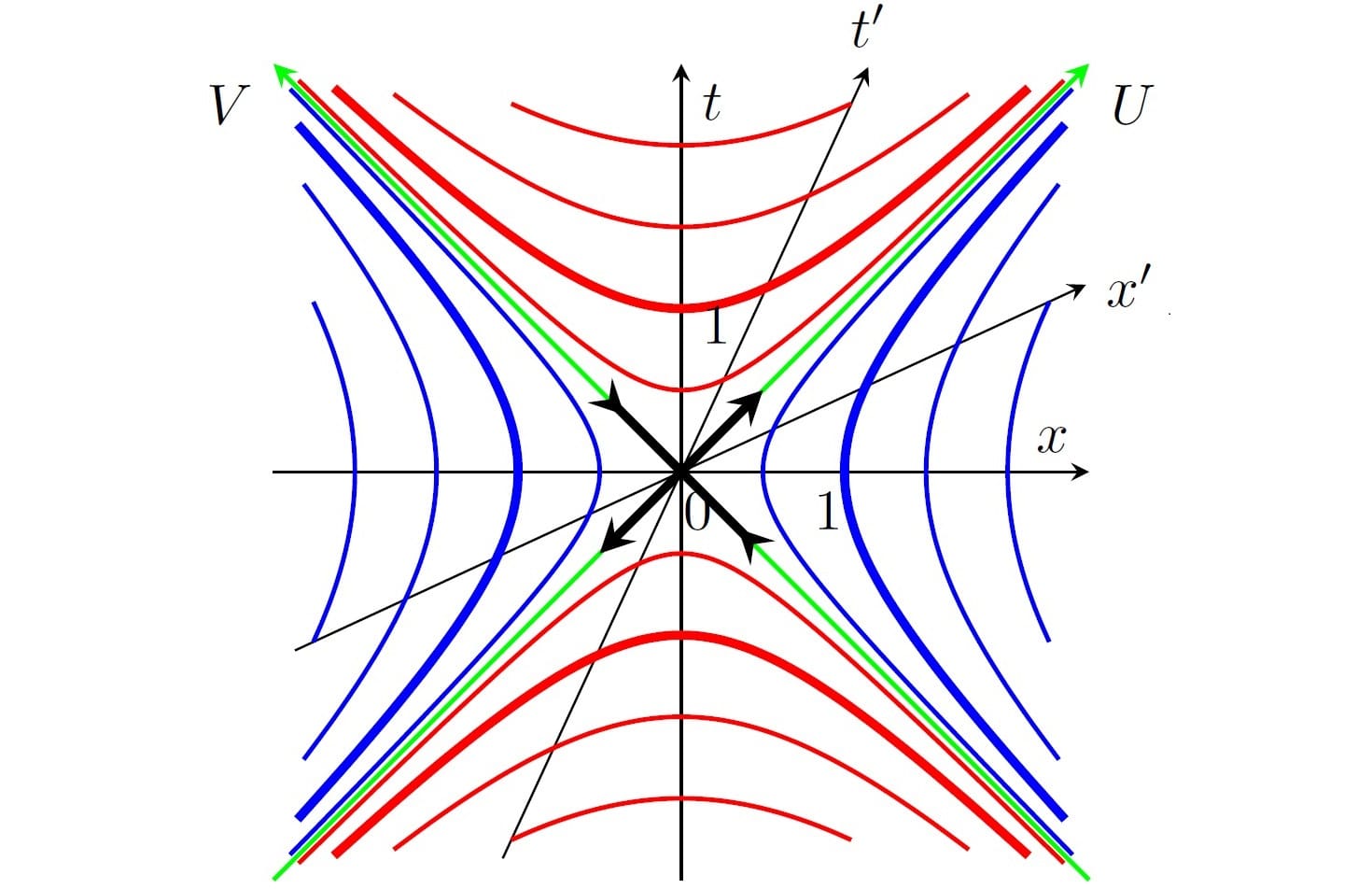
Этот элегантный подход прекрасно работает для обычного пространства. Но пространство-время Эйнштейна — это нечто более сложное. В нем, помимо трех пространственных, есть и временная координата, что кардинально меняет его геометрию. Здесь «расстояние» между событиями может быть не только пространственноподобным, но и времениподобным, и даже светоподобным (нулевым). Из-за этой сложной структуры полная классификация конических сингулярностей в пространстве-времени Минковского оставалась нерешенной задачей. Ученые знали, как описывать простые, времениподобные сингулярности, аналогом которых служат гипотетические космические струны, но избегали более сложных случаев, считая их слишком неоднозначными.
Коллектив физиков в составе Михаила Иванова и Захара Хайдукова решил взяться за эту задачу. Их целью было построить исчерпывающую «периодическую таблицу» всех возможных типов конических сингулярностей, которые могут возникнуть на «швах» пространства-времени Минковского, не ограничиваясь лишь простейшими случаями. Для этого они рассмотрели процесс «склейки» плоских фрагментов пространства-времени не как простое вращение, а как преобразование Лоренца — симметрия, лежащая в основе специальной теории относительности и описывающий, как меняются пространство и время для движущихся наблюдателей. Ученые систематически проанализировали, как можно соединять друг с другом различные секторы плоскости Минковского, разделенные световыми лучами.
Исследователи обнаружили целый «зоопарк» сингулярностей, кардинально отличающихся от ранее известных. Помимо уже знакомых «стандартных» конусов, ученые построили классификацию, включающую «исключительные», «четные» и «нечетные» типы. Самым поразительным открытием стало то, что многие из этих новых, «нестандартных» сингулярностей оказались не просто математическим артефактом приближенного метода. В отличие от стандартных, они не исчезают при переходе к пределу, когда размеры плоских «кусочков» стремятся к нулю. Это означает, что такие сингулярности могут представлять собой фундаментальные, неустранимые особенности самой ткани пространства-времени, которые классическая теория Эйнштейна просто не в состоянии описать.
Михаил Иванов, доцент кафедры теоретической физики МФТИ, прокомментировал: «Исчисление Редже — очень мощный инструмент, но традиционно его применяли как приближенное описание для гладкого пространства-времени. При этом не рассматривались случаи, которые не могут возникнуть при описании гладких поверхностей. Мы решили подойти к проблеме систематически и посмотреть, какие вообще возможны склейки многомерных пирамидок (симплексов) и не отбрасывать «лишние» склейки как нефизические, а попробовать придать им физический смысл. По сути, мы создаем алфавит, с помощью которого можно будет описывать гораздо более широкий класс геометрических конфигураций. Появление комплексного действия — это прямой намек на то, что мы вышли за рамки классической теории гравитации. Эти «нестандартные» конусы могут описывать чисто квантовые явления, например, ветвление пространства-времени, когда из одной точки истории возникает несколько альтернативных будущих, или даже рождение нашей Вселенной из ничего, как в модели Хартла-Хокинга. Наша работа дает математический инструмент для расчета вероятностей таких процессов. Например, мы описали геометрию, при которой частица, двигаясь вдоль замкнутого пути вокруг «нечетного» конуса, может развернуться и начать двигаться вспять по времени. Это не означает, что такое возможно физически, просто мы пока составляем каталог возможных особенностей и смотрим какие из них могут быть полезны как строительные блоки новой теории».
Новый подход не избегает сложностей, а погружается в них. Авторы показали, что предыдущие работы описывали лишь один, самый простой тип конуса из бесконечного разнообразия. Новая классификация впервые дает физикам полный набор «кирпичиков» для построения моделей пространства-времени в рамках дискретного подхода. Более того, исследование показало, что некоторые из этих новых сингулярностей приводят к появлению комплексных чисел в выражении для действия — величины, которая в физике определяет динамику системы. В классической физике действие всегда вещественно, а его мнимая часть указывает на квантовые эффекты, такие как туннелирование или процессы, запрещенные классическими законами.
Это исследование может иметь большое значение для фундаментальной наук. Предложенная классификация открывает дорогу к построению более полных и реалистичных моделей квантовой гравитации. Она позволяет описывать конфигурации с меняющейся топологией и даже с изменением сигнатуры метрики — переходом между евклидовым пространством и пространством Минковского, что важно для теорий, описывающих рождение Вселенной.
В будущем ученые планируют применить разработанный формализм для анализа конкретных физических сценариев, включая квантовые флуктуации ранней Вселенной и поведение материи вблизи экзотических гравитационных объектов. Их работа предоставляет мощный язык для описания мира, в котором сама геометрия пространства и времени подчиняется вероятностным законам квантовой механики.