Результаты исследования опубликованы в журнале IEEE Access. Лазерная интерферометрия позволяет «увидеть» невидимые неоднородности в прозрачных средах, например, распределение плотности в плазме или напряжение в стекле. Интерференционная картина, состоящая из чередующихся светлых и темных полос, несет в себе зашифрованную информацию о фазовом распределении, которое, в свою очередь, напрямую связано с физическими свойствами объекта. Расшифровать эту информацию — ключевая задача для многих областей науки и техники.
Однако на практике этот «снимок волн» почти всегда оказывается несовершенным. Изображение может быть зашумлено, полосы могут иметь сложную, непредсказуемую форму, а их контрастность может быть низкой. Особенно остро эта проблема стоит при изучении динамичных, сверхбыстрых процессов, когда для анализа доступен лишь один-единственный кадр. Существующие методы расшифровки, или «развертки фазы», часто пасуют перед такими трудностями. Классические подходы чувствительны к шуму и могут накапливать ошибки в процессе вычислений, а современные нейросетевые решения, хоть и быстры, часто работают как «черный ящик» и требуют для обучения огромных массивов идеально размеченных данных, которых для уникальных экспериментов попросту не существует.
Перед учеными стоял вызов: создать метод, который был бы одновременно точным, надежным, устойчивым к шуму и физически корректным.
Чтобы преодолеть эти ограничения, российские физики разработали принципиально новый подход — итерационный фреймворк WISP (Workframe for Interferogram Signal Phase-unwrapping). Его главная особенность заключается в том, что он не пытается решить задачу «в лоб» за один проход. Вместо этого WISP запускает итерационный процесс, на каждом шаге которого он последовательно уточняет свое понимание структуры изображения, приближаясь к истинному фазовому распределению. Важнейшее отличие от многих других итерационных алгоритмов состоит в том, что WISP на каждом цикле работает с исходным, нетронутым изображением, что предотвращает накопление ошибок и «замыливание» важных деталей.
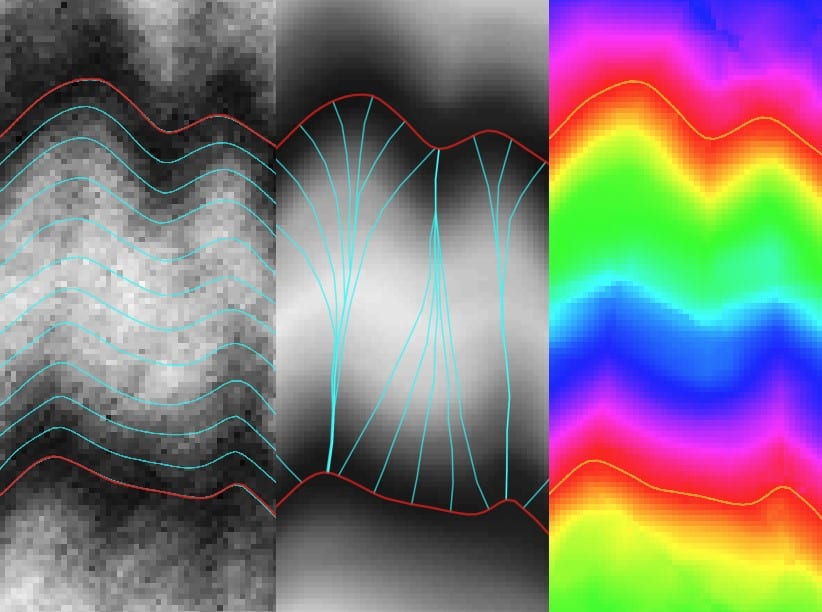
Рисунок 1. Схема итерационного процесса восстановления фазы в рамках фреймворка WISP. Алгоритм начинается с предварительной трассировки темных полос на исходной интерферограмме (пример показан справа). Затем он входит в итерационный цикл, включающий построение линий равной фазы (изофаз), вычисление локальных направлений полос, анизотропное сглаживание для подавления шума и, наконец, развертку фазы. Ключевым элементом является проверка сходимости: если результат недостаточно точен, система использует полученную информацию для более точной трассировки полос и запускает новый цикл уточнения. Процесс завершается, когда достигается максимальное соответствие модели реальному изображению / © T. F. Khirianov et al., IEEE Access. Рисунок был переведен с помощью Claude Sonnet 4
Процесс работы WISP можно разбить на несколько ключевых этапов.
Сначала, используя усовершенствованный параболический метод, алгоритм находит предварительное положение темных интерференционных полос. Затем в дело вступает одно из главных нововведений — оригинальная функция потерь SKIM (Smoothed Kernel-based Intensity Measuring). Она действует как сверхточный наводчик, оценивая, насколько удачно предполагаемая линия соответствует самому темному участку на изображении, и корректирует ее положение с помощью градиентного спуска до достижения идеального совпадения. После этого WISP строит между темными полосами вспомогательные линии равной фазы — изoфазы.
Второй ключевой этап — это «умное» сглаживание. Вместо того чтобы применять стандартные фильтры, которые размывают все изображение целиком, WISP применяет анизотропную диффузию. Этот метод сглаживает шум только вдоль интерференционных полос, но не поперек них. Это можно сравнить с реставрацией картины, где специалист удаляет пыль вдоль мазков кисти, не повреждая саму текстуру. Такой подход позволяет эффективно убрать случайный шум, полностью сохранив резкость и морфологию самих полос, что критически важно для точности. На основе очищенной и структурированной информации алгоритм восстанавливает полную двумерную карту фазы. Затем цикл повторяется: используя полученную на первом шаге карту фазы, WISP проводит еще более точную трассировку полос и изoфаз, снова применяет анизотропное сглаживание и получает еще более точную карту фазы.
Итерации продолжаются до тех пор, пока разница между модельным интерференционным узором, построенным на основе восстановленной фазы, и реальным экспериментальным изображением не достигнет минимума.
Для проверки эффективности своего детища ученые провели серию строгих тестов. Они взяли чистое изображение интерферограммы и добавили к нему белый гауссовский шум различной интенсивности — от едва заметного до такого, при котором амплитуда шума составляла половину от амплитуды полезного сигнала, делая изображение почти нечитаемым для глаза. WISP с честью выдержал это испытание, продемонстрировав выдающуюся робастность. Но самое главное — прямое сравнение с другими передовыми методами, включая алгоритмы, основанные на нейронных сетях. В условиях высокого уровня шума WISP показал себя абсолютным лидером, снизив ошибку восстановления фазы на 39,7% по сравнению с ближайшим конкурентом. Это колоссальное преимущество, которое доказывает превосходство физически обоснованного, итерационного подхода над другими решениями в сложных условиях. Единственной платой за такую точность является время вычислений — WISP работает медленнее нейросетей, однако, как подчеркивают авторы, для анализа уникальных научных данных надежность и точность несравнимо важнее скорости.
Практическая значимость разработки огромна. Новый фреймворк может стать незаменимым инструментом для исследователей, работающих в области физики плазмы, газовой динамики, материаловедения и адаптивной оптики. Например, он позволит детально изучать структуру и динамику плазменных филаментов в наносекундных разрядах, что важно для понимания фундаментальных механизмов пробоя и создания новых плазменных технологий. В промышленности WISP может применяться для высокоточного контроля качества оптических элементов или для исследования напряжений в прозрачных материалах. По сути, это новый мощный инструмент для всей области вычислительной визуализации, позволяющий извлекать максимум полезной информации из несовершенных данных.
В будущем коллектив планирует усовершенствовать алгоритм для работы с еще более сложными случаями интерферограмм, например, с замкнутыми полосами и так называемыми седловыми точками, что еще больше расширит область его применения.